Two solid bodies together?
A uniform disc of mass and radius is kept above a sphere of of mass and radius at a distance of (As shown in figure) such that the line joining the centres of the disc and sphere is perpendicular to the plane of the disc.Find the force of gravitational attraction between the disc and the sphere.
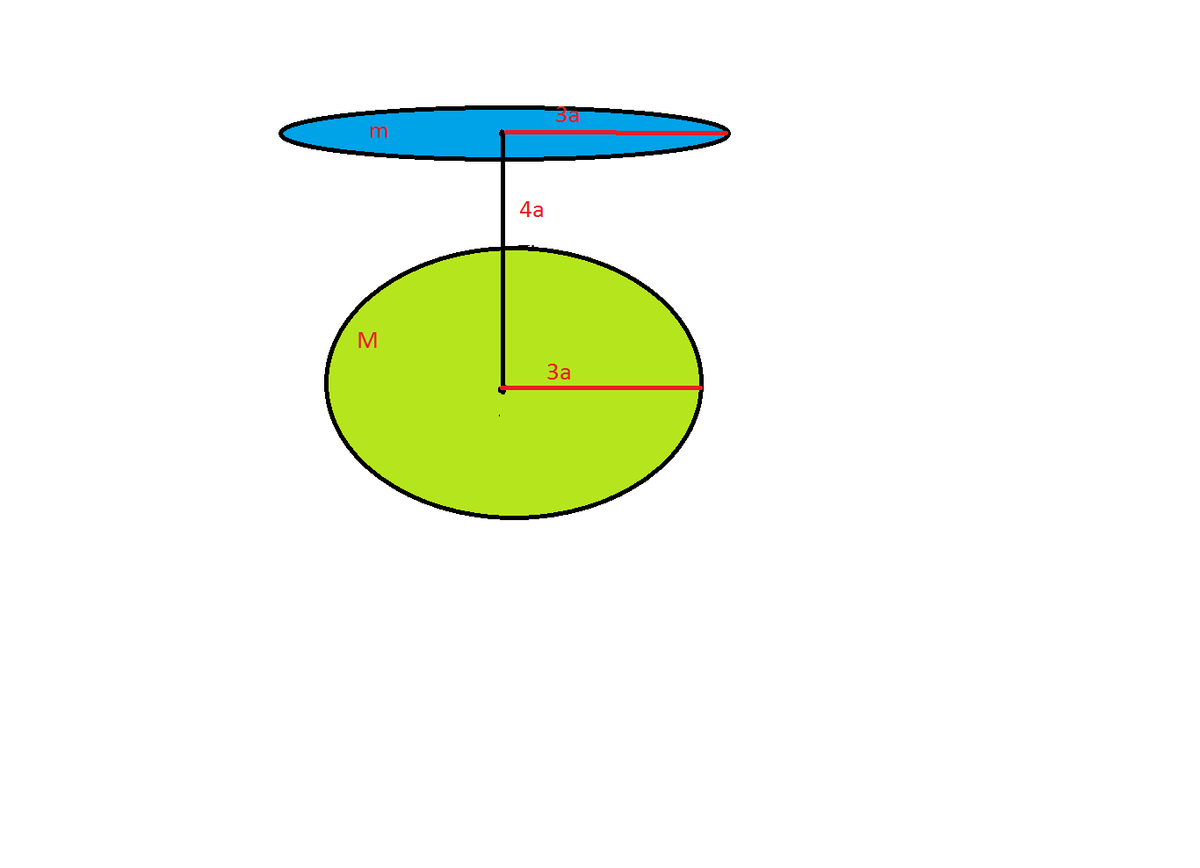
If your answer is of the form , find the value of
Details and Assumptions
-
The distance is the center to center distance.
-
Here is the gravitational constant.
ORIGINAL
Liked it? Try this
The answer is 47.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since the entire disc is outside the radius of the sphere, we can treat the sphere as a point particle. Since the sphere is inside the sphere of radius 3 a that contains the disc, we cannot treat the disc as a point particle. The gravitational attraction between the sphere and the disc will be on a line between the two centres, though. Thinking about a circular disc of radius r inside the disc, the force of gravitational attraction between the two objects is ∫ 0 3 a 1 6 a 2 + r 2 G M 9 π a 2 2 π r d r m × 1 6 a 2 + r 2 4 a = 9 a 8 G M m ∫ 0 3 a ( 1 6 a 2 + r 2 ) 2 3 r d r = 9 a 8 G M m [ − 1 6 a 2 + r 2 1 ] 0 3 a = 9 a 8 G M m ( 4 a 1 − 5 a 1 ) = 4 5 a 2 2 G M m making the answer 2 + 4 5 = 4 7 .