Two solid cylinders

I found it easier to determine the rolling conditions when I changed the sign of $\varphi$ , so I have redrawn the diagram to suit.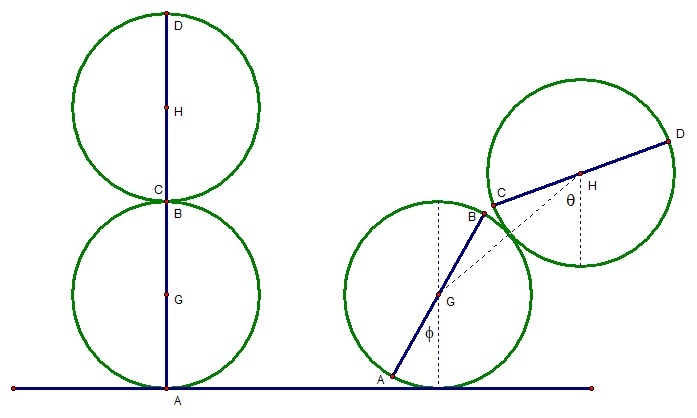 The position vector of the centre of mass $G$ of the bottom cylinder is $\overrightarrow{OG} \; = \; \left(\begin{array}{c} R\varphi \\ R \end{array}\right)$ The position vector of the centre of mass $H$ of the top cylinder is $\overrightarrow{OH} \; = \; \left(\begin{array}{c} R\varphi + 2R\sin\theta \\ R + 2R\cos\theta \end{array} \right)$ (this ensures that there is no slipping) which means that the two centres of mass have velocities $\mathbf{v}_G \; = \; \left(\begin{array}{c} R\dot{\varphi} \\ 0 \end{array} \right) \hspace{2cm} \mathbf{v}_H \; = \; \left(\begin{array}{c} R\dot{\varphi} + 2R\cos\theta\dot{\theta} \\ -2R\sin\theta\dot{\theta} \end{array} \right)$ In addition, the bottom and top cylinders have angular velocities $\dot{\varphi}$ and $2\dot{\theta} - \dot{\varphi}$ respectively. Thus the kinetic energy of the system is $\begin{aligned} T & = \; \tfrac12M(R\dot{\varphi})^2 + \tfrac14MR^2\dot{\varphi}^2 + \tfrac12MR^2\big[(\dot{\varphi} + 2\cos\theta\dot{\theta})^2 + 4\sin^2\theta\dot{\theta}^2\big] + \tfrac14MR^2(2\dot{\theta}-\dot{\varphi})^2 \\ & = \; \tfrac12MR^2\big[3\dot{\varphi}^2 + 6\dot{\theta}^2 + 2(2\cos\theta-1)\dot{\varphi}\dot{\theta}\big] \end{aligned}$ and so the Lagrangian of the system is $\mathcal{L} = T - 2MgR\cos\theta$ . Since $\mathcal{L}$ is independent of $\varphi$ , it follows that $\frac{\partial \mathcal{L}}{\partial \dot{\varphi}}$ is a constant of the motion, and hence we deduce that $3\dot{\varphi} + 2(2\cos\theta-1)\dot{\theta} \; = \; 0$ Conservation of energy now tells us that $\tfrac12MR^2\big[3\dot{\varphi}^2 + 6\dot{\theta}^2 + 2(2\cos\theta-1)\dot{\varphi}\dot{\theta}\big] + 2MgR\cos\theta \; = \; 2MgR$ Substituting $\dot{\varphi} = -\tfrac23(2\cos\theta-1)\dot{\theta}$ into this equation yields the formula $\dot{\theta}^2 \; = \; \frac{12g(1-\cos\theta)}{R(17 + 4\cos\theta - 4\cos^2\theta)}$ making the answer $12 + 17 + 4 + 4 = \boxed{37}$ .

Cylinder rolling on another cylinder is well known problem and the numbers in the expression sum to:

Answer=12+17+4+4=37