Two spheres against a corner in a cube.
Two spheres are placed in the corner of a cube such that a cross-section shows that they are touching each other as well as the walls of the cube as shown in the figure.
If the radius of the larger sphere is R and that of the smaller sphere is r
Calculate r/R to two decimal places.
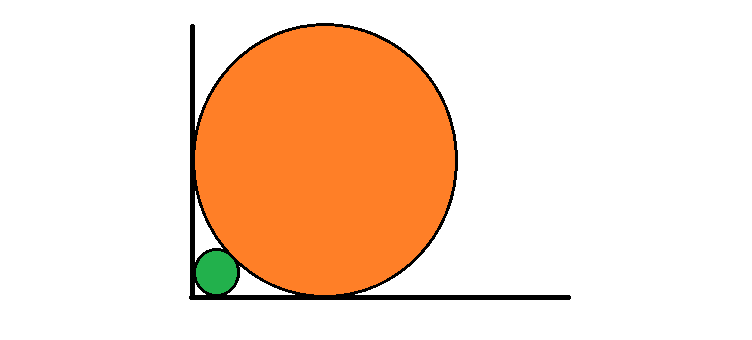
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Distance of the center of the larger sphere from the corner
is sqrt(R^2 + R^2 + R^2) = sqrt(3)*R
Similarly the distance of the center of the smaller sphere from the corner is sqrt(3)*r.
The centres of the spheres lie on the same line which ends in the corner
so
sqrt(3) R = sqrt(3) r + r + R
ie. R(sqrt(3)-1) =r( sqrt(3) + 1)
That gives us r/R = (sqrt(3)-1)/(sqrt(3) + 1)