Googly Eyed Triangle
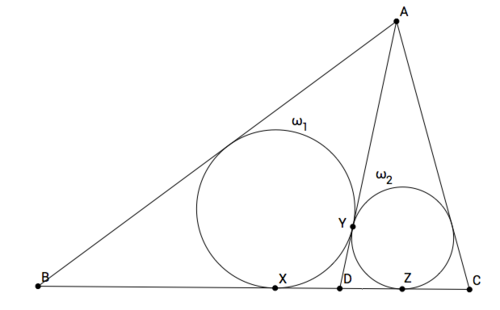 Point
D
is on side
B
C
of
△
A
B
C
.
The incircle
ω
1
of
△
A
B
D
is tangent to
B
C
at
X
and to
A
D
at
Y
.
The incircle
ω
2
of
△
A
D
C
is tangent to
B
C
at
Z
and to
A
D
at
Y
.
If the radius of
ω
1
is
2
,
and the radius of
ω
2
is
1
,
find the value of
X
Y
2
+
Y
Z
2
to the nearest tenth.
Point
D
is on side
B
C
of
△
A
B
C
.
The incircle
ω
1
of
△
A
B
D
is tangent to
B
C
at
X
and to
A
D
at
Y
.
The incircle
ω
2
of
△
A
D
C
is tangent to
B
C
at
Z
and to
A
D
at
Y
.
If the radius of
ω
1
is
2
,
and the radius of
ω
2
is
1
,
find the value of
X
Y
2
+
Y
Z
2
to the nearest tenth.
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
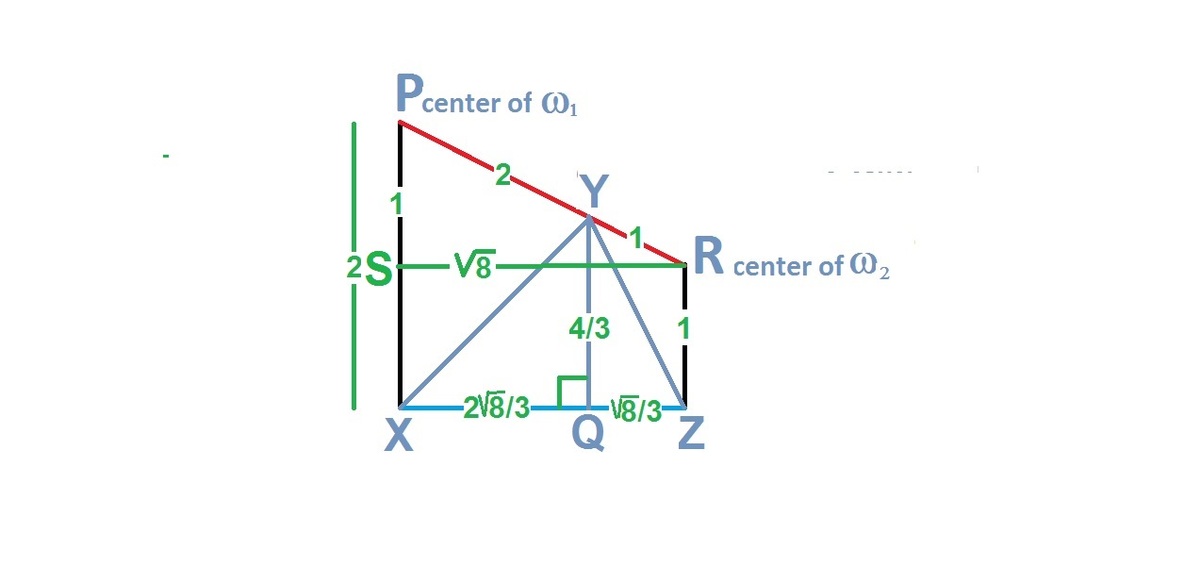 P and R are the centers,
R
S
⊥
P
X
,
Y
Q
⊥
X
Z
.
S
R
=
(
2
+
1
)
2
−
1
2
=
8
,
∴
X
Q
=
3
2
8
,
Z
Q
=
3
1
8
.
Y
Q
=
3
1
P
S
+
S
X
=
3
4
.
X
Y
2
+
Y
Z
2
=
(
X
Q
2
+
Y
Q
2
)
+
(
Z
Q
2
+
Y
Q
2
)
=
8
P and R are the centers,
R
S
⊥
P
X
,
Y
Q
⊥
X
Z
.
S
R
=
(
2
+
1
)
2
−
1
2
=
8
,
∴
X
Q
=
3
2
8
,
Z
Q
=
3
1
8
.
Y
Q
=
3
1
P
S
+
S
X
=
3
4
.
X
Y
2
+
Y
Z
2
=
(
X
Q
2
+
Y
Q
2
)
+
(
Z
Q
2
+
Y
Q
2
)
=
8
Let E be the center of ω 1 and F be the center of ω 2 . Let G be the foot of the perpendicular dropped from F onto E X . We have F G = X Z because F G X Z is a rectangle. Also, E G = 1 and F E = 3 . Solving for F G using right triangle E F G yields F G = X Z = 8 .
Now, from Power of a Point, we deduce that X D = D Y = D Z . This shows that X Y Z is a right triangle, which can be seen by drawing a circle with center D passing through X . Thus, X Y 2 + Y Z 2 = 8 2 = 8 .
N i c e solution. Can you please explain "Power of a point" and equality of three lines? Thanks. I do understand the equality of the three tangent length. it is only with reference of "Power of point" that I need understand.
Log in to reply
Power of a Point states that, given a circle and a point P, and a line passing through P intersecting the circle at points A and B, the product P A ( P B ) is constant. We can use this to show that the tangents are equal.
Log in to reply
Thanks. I did not know the name. I knew this property of the circle. If you do not mind can you please explain how this is applied to show the two tangents to be equal. Thanks.
By LoC, note that we have X Y 2 = 2 r 2 + 2 r 2 cos θ and Y Z 2 = 2 r 2 − 2 r 2 cos θ , giving their sum to be 4 r 2 where r is the tangent length. By Equal Tangents, we note that X D = Z D = r . By Pythagoras, we have that X Z = 2 2 , giving the answer as 8 .