Two Thetas Make a Triangle

Calculus Level 5

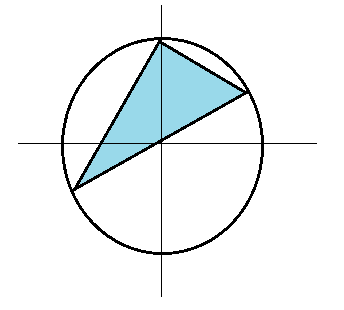
Consider three points on the unit circle in the $x y$ plane:

$\begin{aligned} \vec{P_1} & = (0,1) \\ \vec{P_2} & = ( \cos \theta_1, \sin \theta_1) \\ \vec{P_3} & = ( \cos \theta_2, \sin \theta_2) \end{aligned}$

Angles $\theta_1$ and $\theta_2$ are randomly and uniformly distributed between $0$ and $2 \pi$ . If these three points are the vertices of a triangle, what is the triangle's expected area?

The answer is 0.477.

1 solution

Jose Fernandez Goycoolea
Jun 13, 2018

As usual, I approached the problem numerically. I placed it on the plane as in the figure so that:

${\bf P_1} = (~\cos(\alpha),~1+\sin(\alpha)~)$

${\bf P_2} = (~\cos(\beta),~1+\sin(\beta)~)$

for the randomly and uniformly distributed angles $\alpha,\beta\in[0,2\pi]$ . With this conventions, the area of the triangle is given by

$A=\frac1{2}|\mbox{det}({\bf P_1},{\bf P_2})| = \frac1{2}|\cos(\alpha) + \sin(\beta - \alpha) - \cos(\beta)|$

from here I write some code and estimated the expected area throughout the mean $\overline{A}\approx\boxed{0.477}$

import math
from random import uniform as rand
from statistics import mean as mean

N = 10**7
area = []
for i in range(0,N):
    a = rand(0,2*math.pi)
    b = rand(0,2*math.pi)
    area.append( abs(math.cos(a) + math.sin(b - a) - math.cos(b)) / 2 )
print(mean(area))

But is there no other way of doing it? The topic of the question is calculus

Jaya Krishna - 2 years, 12 months ago

Continuing without code we would have to calculate an integral.

Let ${\bf x}=(\alpha,\beta)\in[0,2\pi]\times[0,2\pi]=D$ then $E[A]=\int_DA({\bf x})f({\bf x})d{\bf x}$ sice we are choosing a point uniformly at random from a square of side $2\pi$ the probability dencity function is just $f({\bf x})=\frac1{4\pi^2}$ hence our integral is $E[A]=\int_0^{2\pi}\int_0^{2\pi}\frac{|\cos(\alpha) + \sin(\beta - \alpha) - \cos(\beta)|}{8\pi^2}d\alpha d\beta=\frac{3}{2\pi}\approx\boxed{0.477}$

The code above is actually solving this integral numerically in a pretty weird way :)

Jose Fernandez Goycoolea - 2 years, 12 months ago

Is there some way to remove mod from this integral? I tried integrating $\alpha$ from $0 \to \beta$ and switching one factor of $2\pi \to \beta$ but that gave 0.306 as answer

Manoj 420 - 2 years, 12 months ago

Yes, there is. The sign of $\mbox{det}({\bf P_1},{\bf P_2})$ depends on the orientation of the vectors ${\bf P_1}$ and ${\bf P_2}$ the problem is that I made a poor choice on the parametrization if one want to solve by hand. My angles $\alpha$ and beta $\beta$ are measured from the point $(0,1)$ and not from the origin. It would be better to use:

${\bf P_1} = (~\sin(\alpha),~1-\cos(\alpha)~)$

${\bf P_2} = (~\sin(\beta),~1-\cos(\beta)~)$

In this way $\mbox{det}({\bf P_1},{\bf P_2})=\sin(\alpha)-\sin(\alpha - \beta) -\sin(\beta)>0$ exactly when $\alpha>\beta$ since the angles coincide with the directions of the vectors. Finally since the integral is simmetrical on both triangles (of the $\alpha\beta$ -square) it reduces to

$E[A]=\int_0^{2\pi}\int_0^{2\pi}\frac{|\sin(\alpha)-\sin(\alpha - \beta) -\sin(\beta)|}{8\pi^2}d\beta d\alpha = 2\int_0^{2\pi}\int_{\alpha}^{2\pi}\frac{\sin(\alpha)-\sin(\alpha - \beta) -\sin(\beta)}{8\pi^2} d\beta d\alpha =\frac{3}{2\pi}\approx\boxed{0.477}$

Jose Fernandez Goycoolea - 2 years, 12 months ago

Two Thetas Make a Triangle

The answer is 0.477.

1 solution

0 pending reports