Two-tone Pinwheel
In a quadrilateral A B C D in which ∠ A B D = ∠ B D C = 4 0 ∘ and ∠ B C A = ∠ C A D = 4 5 ∘ , find the smaller of the two angles between the diagonals.
Report the positive difference between the two solutions to this problem.
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions

Since there are two pairs of equal alternate interior angles, quadrilateral A B C D is a parallelogram. See the figure above; let O P = P A = O Q = Q C = 1 and ∠ D Q P = θ . We note that:
tan ( 9 0 ∘ − θ + 4 0 ∘ ) ⟹ tan ( 1 3 0 ∘ − θ ) tan ( 5 0 ∘ + θ ) 1 − tan 5 0 ∘ tan θ tan 5 0 ∘ + tan θ = D E E C = D P − E P 2 = tan θ − 1 2 = 1 − tan θ 2 = 1 − tan θ 2 As tan ( 1 8 0 ∘ − x ) = − tan x
tan 5 0 ∘ + tan θ − tan 5 0 ∘ tan θ − tan 2 θ tan 2 θ − ( 1 + tan 5 0 ∘ ) tan θ + 2 − tan 5 0 ∘ = 2 − 2 tan 5 0 ∘ tan θ = 0
Solving the quadratic equation we get θ = { 5 9 . 8 6 3 ∘ 2 5 . 1 3 7 ∘ , then the angle between the diagonals = { 5 9 . 8 6 3 ∘ + 4 5 ∘ = 1 0 4 . 8 6 3 ∘ 2 5 . 1 3 7 ∘ + 4 5 ∘ = 7 0 . 1 3 7 ∘ ; the smaller ones = { 1 8 0 ∘ − 1 0 4 . 8 6 3 ∘ = 7 5 . 1 3 7 ∘ 7 0 . 1 3 7 ∘ and the difference = 7 5 . 1 3 7 ∘ − 7 0 . 1 3 7 ∘ = 5 ∘ .
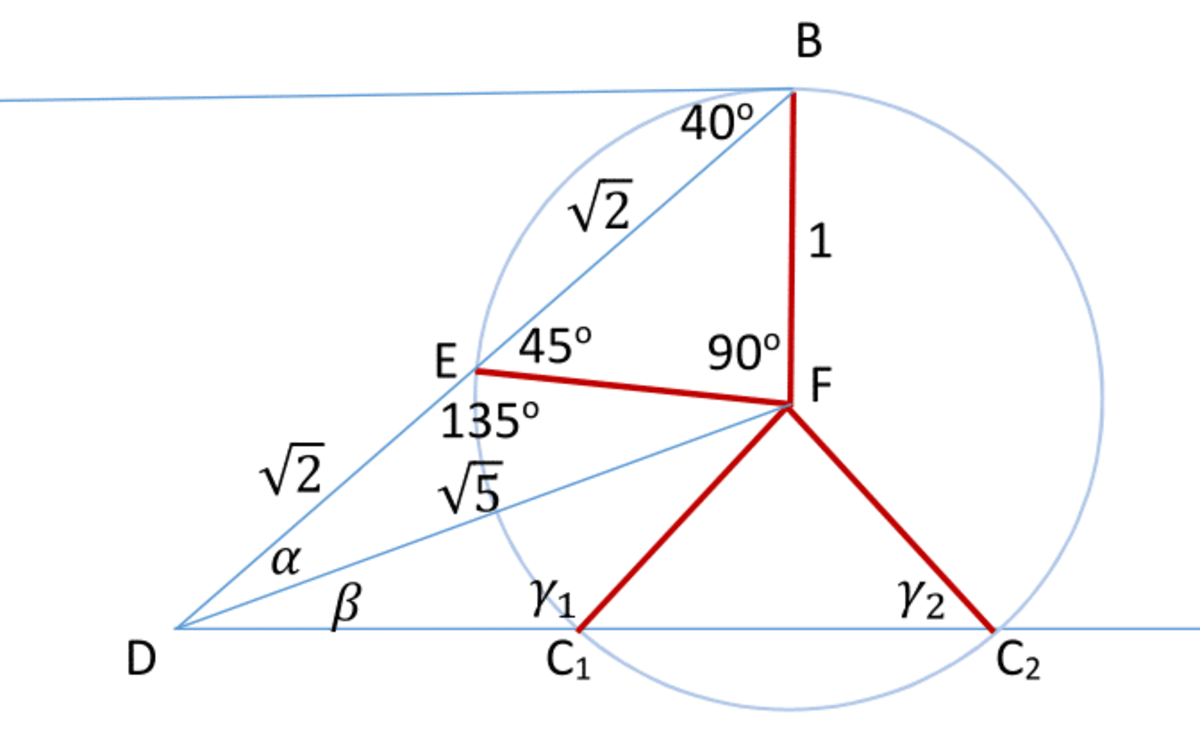 We'll start constructing the solution by drawing points DB and the directions,
4
0
∘
off from the diagonal
D
B
, of the sides DC and AB. The second diagonal will go through point E midway between D and B, due to the symmetry of the problem.
∠
E
C
B
should be
4
5
∘
. We can think of this as the inscribed angle inside a circle going through E, B, and C. Corresping central angle of
9
0
∘
makes locating the center F trivial.
We'll start constructing the solution by drawing points DB and the directions,
4
0
∘
off from the diagonal
D
B
, of the sides DC and AB. The second diagonal will go through point E midway between D and B, due to the symmetry of the problem.
∠
E
C
B
should be
4
5
∘
. We can think of this as the inscribed angle inside a circle going through E, B, and C. Corresping central angle of
9
0
∘
makes locating the center F trivial.
Let's set the radius of the circle arbitrarily at 1. This will give us E B = E D = 2 . In the △ D E F we know also ∠ D E F = 1 3 5 ∘ and E F = 1 . From the law of cosines we get the remaining side as D F = 5 , and the law of sines will then give us angle α = 1 8 . 4 3 5 ∘ .
Switching to △ D F C we know angle β = 4 0 − α = 2 1 . 5 6 5 ∘ , D F = 5 , and F C = 1 . We can look for angle γ using the law of sines.
s i n ( γ ) = 5 × s i n ( 2 1 . 5 6 5 )
There are two solutions: γ 1 = 1 2 4 . 7 2 6 ∘ and γ 2 = 5 5 . 2 7 4 ∘ . Law of cosines applied to △ D F C will give us D C 1 = 1 . 5 0 9 9 and D C 2 = 2 . 6 4 9 2 .DEC
We now switch to the △ D E C as it is the ∠ D E C , or its supplementary angle, that we need to find. We know ∠ E D C = 4 0 ∘ , E D = 2 and the side D C has one of the above values. Law of cosines provides E C 1 = 1 . 0 0 4 1 3 and E C 2 = 1 . 8 1 0 5 9 . Law of sines applied to the △ D E C will then give us the angle between the diagonals. Using inverse sine function will automatically provide the smaller of those two angles.
∠ D E C 1 = a r c s i n ( s i n ( 4 0 ) × 1 . 5 0 9 9 / 1 . 0 0 4 1 3 ) = 7 5 . 1 3 6 9
∠ D E C 2 = a r c s i n ( s i n ( 4 0 ) × 2 . 6 4 9 2 / 1 . 8 1 0 5 9 ) = 7 0 . 1 3 6 9
The difference is 5.
Looking at the nice, round answer, which just happens to be equal to the difference between 40 and 45 degrees, I strongly suspect that there is a far more elegant solution to this problem.
How did you get 85-x? If we consider triangle DAB, angle PAB = 180 - 45 - 40 - x = 95 - x. It must be 95 - x.
I am not sure how you did "graphing." What I did was use the formula for sin of difference for sin(85-x), that gave me equation in sin(x), which I then solved and obtained two solutions which were indeed sin(40) and sin(45).
Log in to reply
There are two ways to do draw the graph.
1] Draw graph of SinX/Sin40 - Sin45/Sin(85 - X). I get four values. Two intersection with y=0 are invalid.
2] Draw two graphs . SinX/Sin40=0 and Sin45/Sin(85 - X)=0. I get two intersection with y=0.
It was also possible to have SinX * {Sin85 * CosX - CosX * Sin85} =Sin40 * Sin45 and solve.
This is true, but why should it be the angle between the diagonals? For this to actually be a solution, you would need to show that it is.
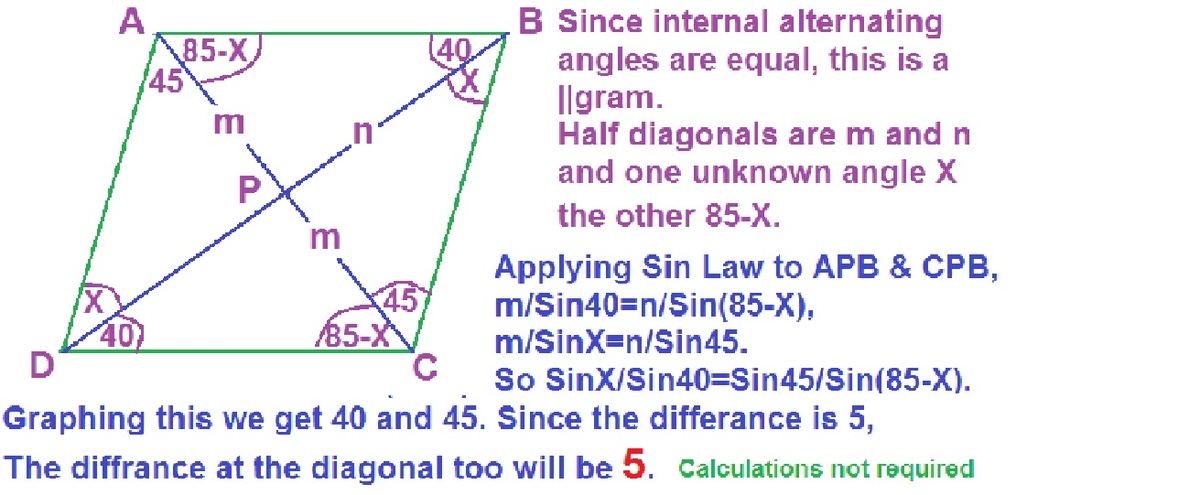
Let the intersection of the diagonals be O .
Note that A O B and C O D are similar ( ∠ A B O = ∠ C D O , ∠ A O B = ∠ C O D ), and so as B O C and D O A . Let A O = x , B O = y , C O = z , then D O = z ⋅ x y = x y z by similarity, and furthermore A O = x y z ⋅ y z = x z 2 by similarity. Thus x = x z 2 ; since x , z > 0 , we have x = z , so A O = C O . Thus A O B and C O D are in fact congruent, and so as B O C and D O A . Thus C O = x , D O = y .
Let ∠ B A O = α , ∠ C B O = β . Note that α + β = 9 5 ∘ because the sum of all internal angles must be 3 6 0 ∘ . By sine rule,
sin ∠ A B O A O = sin ∠ B A O B O ⟹ sin 4 0 ∘ x = sin α y
Similarly, from B O C we can conclude sin β x = sin 4 5 ∘ y . Thus y x = sin α sin 4 0 ∘ = sin 4 5 ∘ sin β . Cross-multiplying, we have sin α sin β = sin 4 0 ∘ sin 4 5 ∘
Remember that α + β = 9 5 ∘ . Thus,
cos 9 5 ∘ cos α cos β = cos ( α + β ) = cos α cos β − sin α sin β = cos α cos β − sin 4 0 ∘ sin 4 5 ∘ = cos 9 5 ∘ + sin 4 0 ∘ sin 4 5 ∘
Thus, we can compute α − β :
cos ( α − β ) = cos α cos β + sin α sin β = ( cos 9 5 ∘ + sin 4 0 ∘ sin 4 5 ∘ ) + sin 4 0 ∘ sin 4 5 ∘ = cos 9 5 ∘ + 2 sin 4 0 ∘ sin 4 5 ∘
Let's go back to the problem. We want to find the difference between the two solutions. We know that ∠ A O B = 1 4 0 ∘ − α , ∠ B O C = 1 3 5 ∘ − β . We want the minimum of these two. Their sum is 2 7 5 ∘ − ( α + β ) = 2 7 5 ∘ − 9 5 ∘ = 1 8 0 ∘ , so whichever is less than 9 0 ∘ , we take it. In other words, if α > 5 0 ∘ (and thus β < 4 5 ∘ ), then we take ∠ A O B , otherwise we take ∠ B O C .
The trick is to realize that the two solutions might make ∠ A O B smaller in one solution, and ∠ B O C smaller in the other! In the above, we see that if α > 5 0 ∘ , we take ∠ A O B . But α − β = 2 α − ( α + β ) = 2 α − 9 5 ∘ . Thus if α − β > 5 ∘ , we take ∠ A O B , otherwise we take ∠ B O C . We know the value of cos ( α − β ) as above; it just suffices to show that cos ( α − β ) = cos 9 5 ∘ + 2 sin 4 0 ∘ sin 4 5 ∘ < cos 5 ∘ , which would imply that ∣ α − β ∣ > 5 ∘ , so one of its two values will be greater than 5 ∘ . (The other will be negative and hence obviously less than 5 ∘ .)
This can be shown in a few ways. One that comes to my mind is this:
We know
cos 9 5 ∘ = − cos 8 5 ∘ = − cos ( 4 5 ∘ + 4 0 ∘ ) = − cos 4 0 ∘ cos 4 5 ∘ + sin 4 0 ∘ sin 4 5 ∘
Also, we know
cos 5 ∘ = cos ( 4 5 ∘ − 4 0 ∘ ) = cos 4 0 ∘ cos 4 5 ∘ + sin 4 0 ∘ sin 4 5 ∘
Thus,
( cos 9 5 ∘ + 2 sin 4 0 ∘ sin 4 5 ∘ ) − ( cos 5 ∘ ) = ( − cos 4 0 ∘ cos 4 5 ∘ + 3 sin 4 0 ∘ sin 4 5 ∘ ) − ( cos 4 0 ∘ cos 4 5 ∘ + sin 4 0 ∘ sin 4 5 ∘ ) = − 2 ( cos 4 0 ∘ cos 4 5 ∘ − sin 4 0 ∘ sin 4 5 ∘ ) = − 2 cos 8 5 ∘ < 0
This proves the claim. Since ∣ α − β ∣ > 5 ∘ , the two solutions have ∠ A O B smaller in one solution, and ∠ B O C smaller in the other.
Let the two solutions for α , β be ( α 1 , β 1 ) , ( α 2 , β 2 ) such that α 1 − β 1 > 0 (and thus α 2 − β 2 < 0 . From the above, we know that α 1 − β 1 > 5 ∘ , so this solution makes ∠ A O B = 1 4 0 ∘ − α 1 as the smaller angle. The second solution has α 2 − β 2 < 0 < 5 ∘ , so this solution makes ∠ B O C = 1 3 5 ∘ − β 2 as the smaller angle. We're looking for their difference; that is, ∣ ( 1 4 0 ∘ − α 1 ) − ( 1 3 5 ∘ − β 2 ) ∣ .
But we know that α 1 − β 1 = − ( α 2 − β 2 ) , and α 1 + β 1 = α 2 + β 2 (both are 9 5 ∘ ). Thus we can in fact conclude that α 1 = β 2 , and so their difference is ∣ ( 1 4 0 ∘ − α 1 ) − ( 1 3 5 ∘ − β 2 ) ∣ = 1 4 0 ∘ − 1 3 5 ∘ = 5 ∘ .