Two Twin Twirls
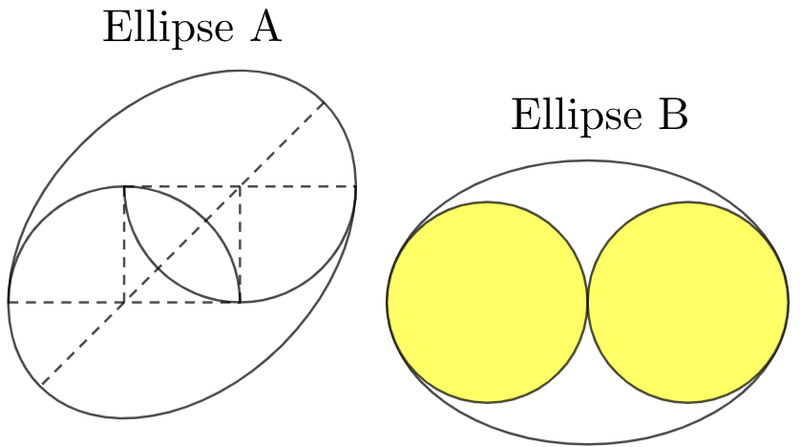
In ellipse , two identical small semicircles are positioned clockwise with respect to the center of the ellipse and the major axis (as shown above), where their centers lie. Two opposite intersection points and two centers altogether form a square of a side length that is the radius of the semicircle. In addition, each semicircle shares exactly one point of tangency with the ellipse.
In ellipse , two tangential yellow circles whose areas are maximum possible and whose diameters exist along the major axis each share one point of tangency at their end.
If both ellipse and ellipse have maximum eccentricities, which of the following must be true?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Ellipse A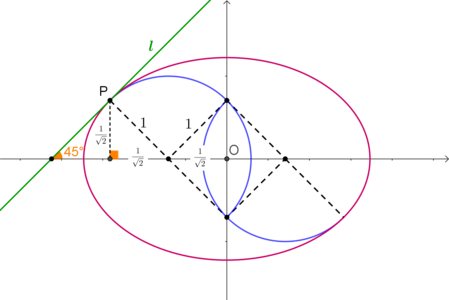 Figure 1
As seen in figure 1, we place ellipse
A
on a coordinate system. The major axis lies on
x
′
x
its center is the origin. We set the radius of each semicircle equal to
1
. In this setting, it is easy to see that the coordinates of point
P
are
(
−
2
,
2
1
)
.
Figure 1
As seen in figure 1, we place ellipse
A
on a coordinate system. The major axis lies on
x
′
x
its center is the origin. We set the radius of each semicircle equal to
1
. In this setting, it is easy to see that the coordinates of point
P
are
(
−
2
,
2
1
)
.
Let the equation of ellipse B be a 2 x 2 + b 2 y 2 = 1 . Then the equation of the tangent l to the ellipse at P is a 2 x P x + b 2 y P x = 1 ⇔ a 2 − 2 x + c 2 1 x = 1 ⇔ 2 b 2 x − a 2 y + 2 a 2 b 2 = 0 Hence, the slope of l is m l = a 2 2 b 2 ( 1 ) At the same time, for the ellipse to have maximum eccentricity, l must be tangent to the semicircle and in this case we have m l = tan 4 5 ∘ = 1 ( 2 )
From ( 1 ) and ( 2 ) we get a 2 2 b 2 = 1 ⇒ a 2 b 2 = 2 1 ⇒ 1 − a 2 b 2 = 1 − 2 1 ⇒ 1 − a 2 b 2 = 2 1 ⇒ e = 2 1
Ellipse B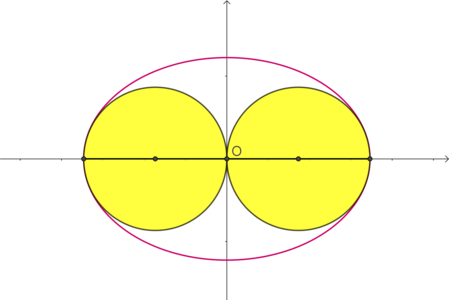 Figure 2
Referring to figure 2, let the equation of ellipse
B
be
a
2
x
2
+
b
2
y
2
=
1
.
Figure 2
Referring to figure 2, let the equation of ellipse
B
be
a
2
x
2
+
b
2
y
2
=
1
.
Then, the radius of curvature at the ends of the major axis is R = a b 2 In order for the yellow circles to be tangent to the ellipse, this value must be greater than or equal to the radius of the circles, which in turn is 2 a , i.e. a b 2 ≥ 2 a .
Consequently, a 2 b 2 ≥ 2 1 ⇒ 1 − a 2 b 2 ≤ 1 − 2 1 ⇒ 1 − a 2 b 2 ≤ 2 1 ⇒ e ≤ 2 1 Since the ellipse has maximum eccentricity, it holds e = 2 1
It is clear that both ellipse A and ellipse B have the same eccentricity.