Valentines Day Problem 1.
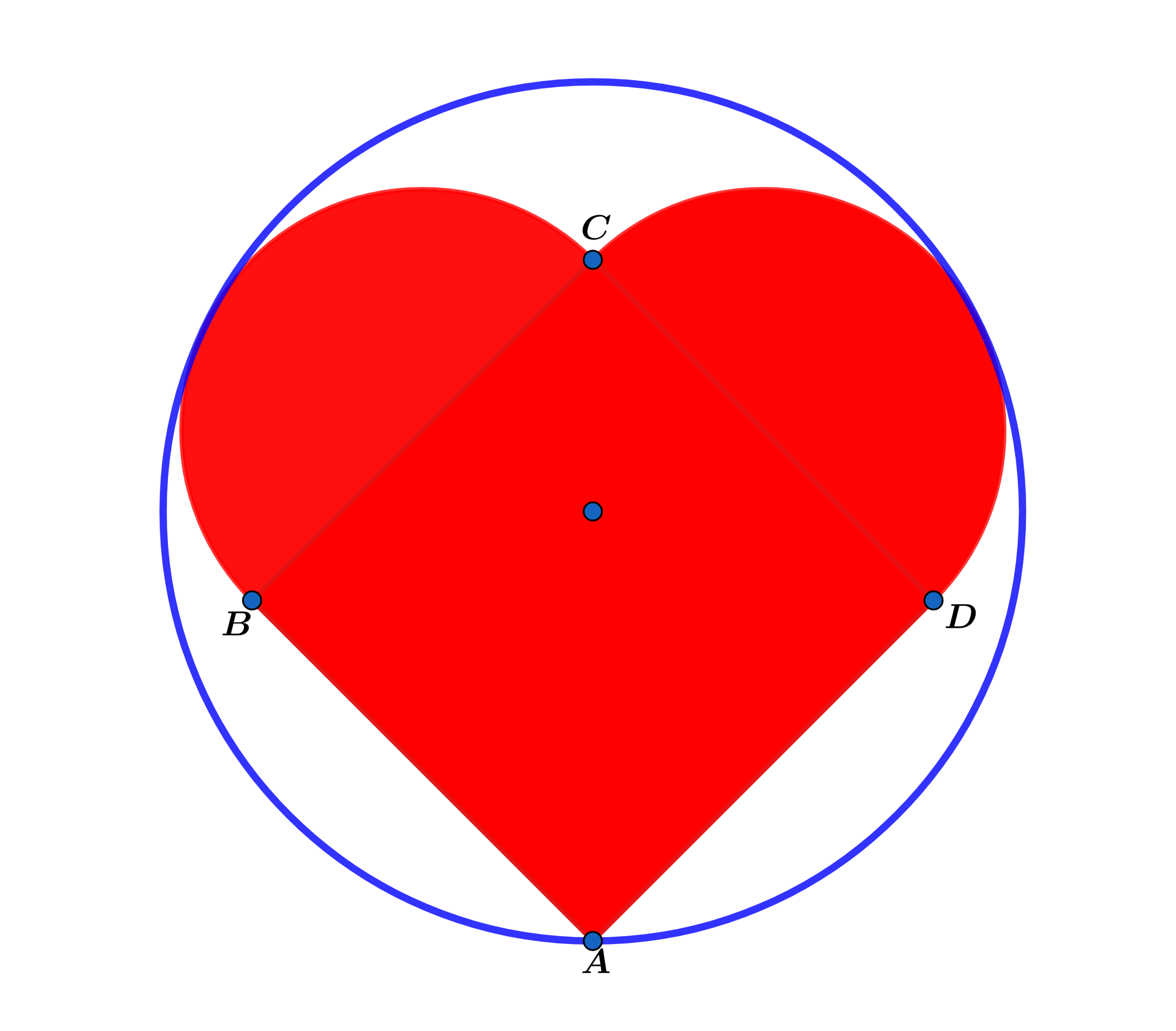
A B C D is a square and B C and C D are diameters of both red semicircles and the heart formed is inscribed in the blue circle and tangent to both red circles as shown above and the blue circle intersects the heart at vertex A of the square.
Let A c and A s be the areas of the blue circle and the square respectively.
If A s A c = ω α ( β + γ α ) π , where α , β , γ and ω are coprime positive integers, find α + β + γ + ω .
The answer is 68.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Label the diagram as follows, and let the sides of the square be s and the radius of the blue circle be r .
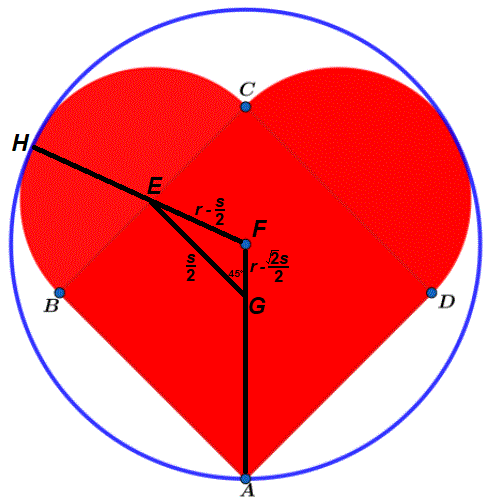
By the properties of a square, E G = E B = E C = E H = 2 s , G A = 2 2 s , and ∠ E G F = 4 5 ° .
Then E F = H F − H E = r − 2 s and F G = F A − G A = r − 2 2 s .
By the law of cosines on △ E F G , E F 2 = E G 2 + F G 2 − 2 ⋅ E G ⋅ F G ⋅ cos ∠ E G F , or ( r − 2 s ) 2 = ( 2 s ) 2 + ( r − 2 2 s ) 2 − 2 ⋅ ( 2 s ) ⋅ ( r − 2 2 s ) ⋅ cos 4 5 ° , which solves to r = 7 2 + 3 2 s .
Therefore, A s A c = s 2 π r 2 = s 2 π ( 7 2 + 3 2 s ) 2 = 4 9 2 ( 1 1 + 6 2 ) π , so that α = 2 , β = 1 1 , γ = 6 , ω = 4 9 , and α + β + γ + ω = 6 8 .
Using the diagram above and the law of cosines on △ C E F with included m ∠ E C F = 4 5 ∘ we have:
( r − 2 a ) 2 = ( 2 a − r ) 2 + 4 a 2 − 2 ( 2 a ) ( 2 2 a − r ) ⟹
4 r 2 − 4 a r + a 2 = 8 a 2 − 8 2 a r − 4 r 2 + a 2 − 2 2 a ( 2 a − r ) ⟹
− 4 a r = − 6 2 a r + 4 a 2 ⟹ 2 ( 3 2 − 2 ) a r = 4 a 2 ⟹ r = 7 3 2 + 2 a
⟹ A s A c = 4 9 ( 3 2 + 2 ) 2 π = 4 9 2 ( 1 1 + 6 2 ) π =
ω α ( β + γ α ) π ⟹ α + β + γ + ω = 6 8 .