Twofer, Part Two
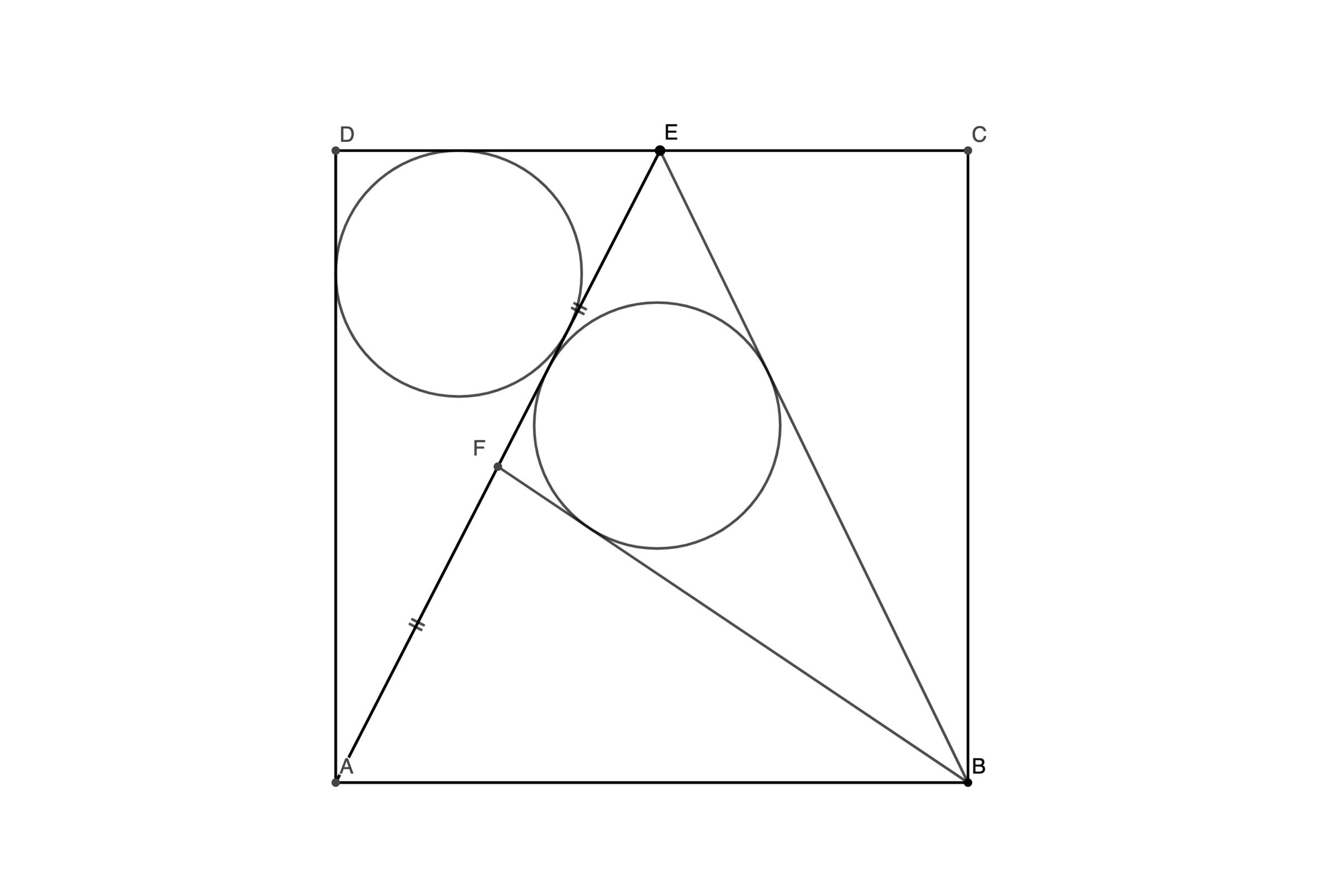
is the unit square. is the midpoint of . is chosen so the two incircles are congruent. If is a root of , where are coprime integers, find .
The answer is 1271.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let's plot this on a Cartesian plane with coordinates A ( 0 , 0 ) , B ( 1 , 0 ) , C ( 1 , 1 ) , D ( 0 , 1 ) , E ( t , 1 ) , F ( 2 t , 2 1 )
By Pythagorean theorem , A E = 1 + t 2 .
The radius on an incircle of a triangle is given to be r = s A , where A and s are the area and semiperimeter of the triangle.
In this case, the radius of incircle of triangle A D E is r : = ( 2 1 ⋅ 1 ⋅ t ) ÷ ( 2 1 + t + 1 + t 2 ) = 1 + t + 1 + t 2 t ( 1 )
Likewise, we can compute the radius of the incircle of triangle E F B , r = semiperimeter of triangle E F B Area of triangle E F B ( 2 )
We can compute the area of the triangle E F B by simply finding the complementary areas. That is, 1 − [ E F B ] = [ D E A ] + [ F A B ] + [ E B C ]
Simplify all these, we get Area of triangle E F B = 4 1 .
Using the distance formula, we can find all the lengths of the triangle F B E . And so (after some tedious algebra) we can obtain its semiperimeter to be 4 1 ( 1 + t 2 + t 2 − 4 t + 5 + 2 t 2 − 2 t + 2 )
Substitute these expressions into ( 2 ) , we get r = 1 + t 2 + t 2 − 4 t + 5 + 2 t 2 − 2 t + 2 1 ( 3 )
Because ( 1 ) = ( 3 ) ,
t ( 1 + t 2 + t 2 − 4 t + 5 + 2 t 2 − 2 t + 2 ) = 1 + t + t 2 + 1
Through repeated squaring and plenty of oh-so-tedious algebraic manipulation, we (magically) arrive at 3 2 t 9 − 2 0 8 t 8 + 6 5 6 t 7 − 1 2 3 6 t 6 + 1 5 6 8 t 5 − 1 4 3 6 t 4 + 9 4 8 t 3 − 3 4 4 t 2 − 1 0 8 t + 7 9 = 0 .
Hence, f ( x ) = ± ( 3 2 x 9 − 2 0 8 x 8 + 6 5 6 x 7 − 1 2 3 6 x 6 + 1 5 6 8 x 5 − 1 4 3 6 x 4 + 9 4 8 x 3 − 3 4 4 x 2 − 1 0 8 x + 7 9 ) ⇒ ∣ f ( 2 ) ∣ = 1 2 7 1 .