Typical Indefinite Integration 2
∫ x ln ( x ) ln ( x ) [ ln ( x ) ( ln ( ln ( x ) ) + 1 ) + 1 ] d x
Ignoring the constant of integration, if the integral above can be expressed as ( f ( x ) ) f ( x ) + 1 , then find the value of f ( e ) .
The answer is 1.000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Kenny Lau How ln ( x ) ln ( x ) + 1 can be equal to 1 ?
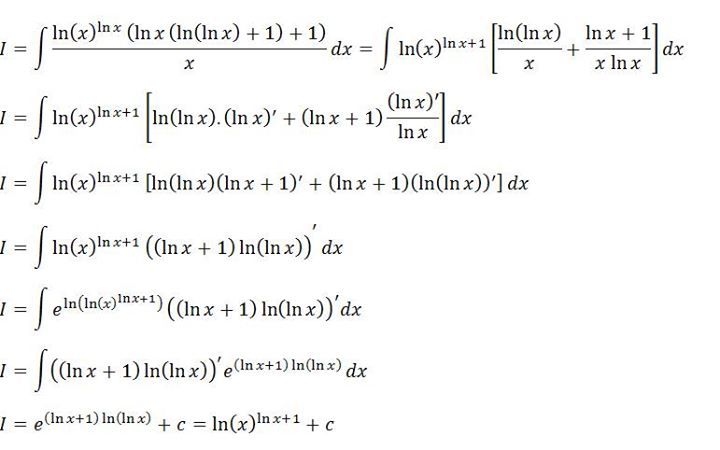
Therefore, f ( x ) = ln ( x ) and so, our answer turns out to be 1
Since there's ln ( x ) everywhere, it's better to let x = e y then use the fact that ( y y ) ′ = y y ( ln ( y ) + 1 ) . The answer should be immediate afterwards.
∫ x ln ( x ) ln ( x ) [ ln ( x ) ( ln ( ln ( x ) ) + 1 ) + 1 ] d x
= ∫ ( ln ( x ) ln ( x ) [ ln ( x ) ( ln ( ln ( x ) ) + 1 ) + 1 ] ) x 1 d x
Let u = ln ( x ) , then d u = x 1 d x .
= ∫ u u [ u ( ln ( u ) + 1 ) + 1 ] d u
= ∫ u u u ( ln ( u ) + 1 ) d u + ∫ u u d u
Let y = u u , then d y = u u ( ln ( u ) + 1 ) d u .
= ∫ u d y + ∫ y d u
Integration by parts.
= u y − ∫ y d u + ∫ y d u
= u y
= u × u u
= u u + 1
= ln ( x ) ln ( x ) + 1