Ugly problem that works out nicely

Geometry Level pending

The current year is 2016. The last year number which was a perfect square was 1936 and before that, 1849.

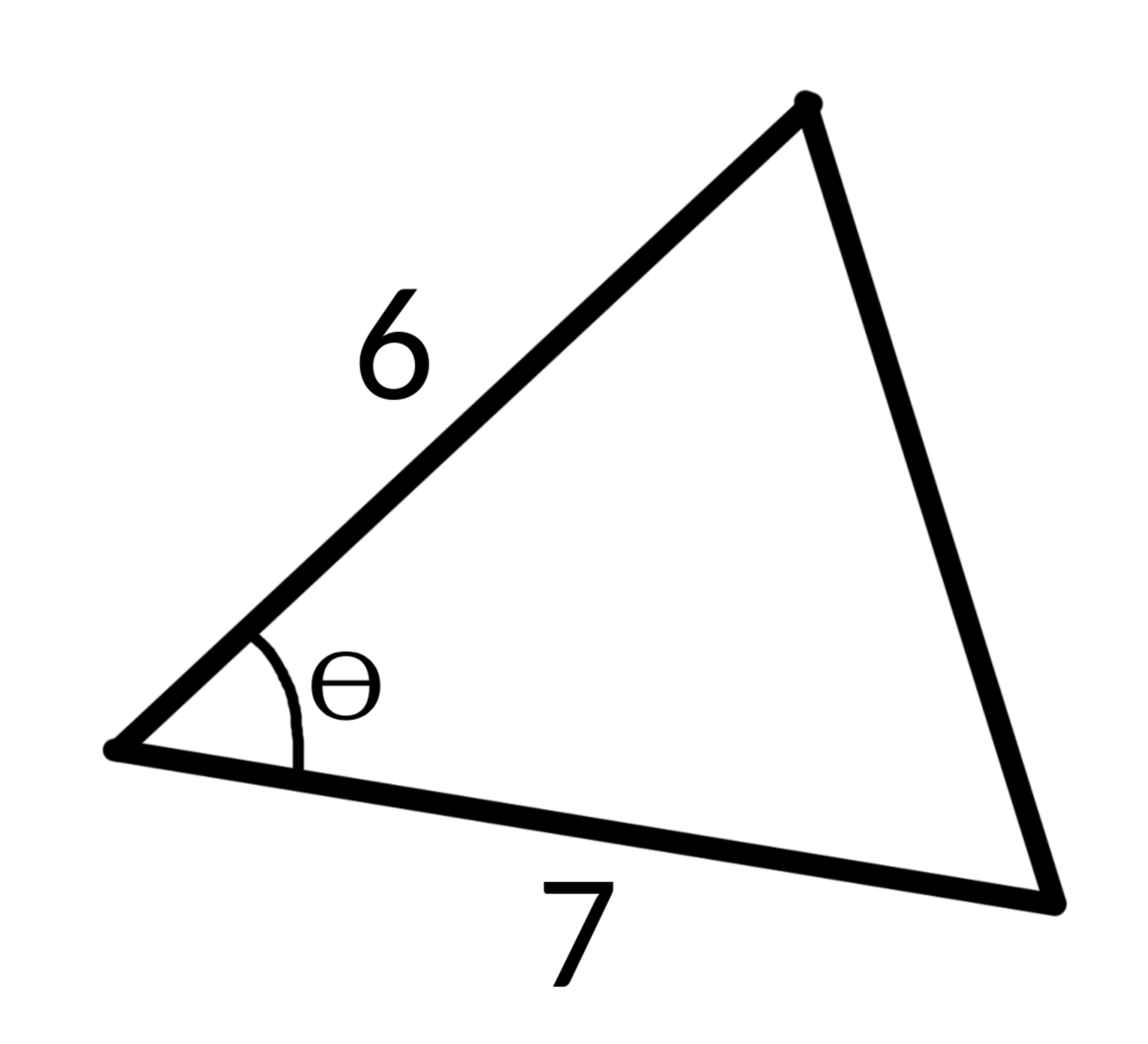
If $\theta =\log _{ \sqrt [ 30 ]{ 45 } }{ x }$ (logarithim with base $\sqrt [ 30 ]{ 45 }$ ) in degrees, where $x$ is the next perfect-square year number, then the area of the triangle below can be written as $\frac { a\sqrt { b }}{ c }$ , where $a$ , $b$ , and $c$ are positive integers, with $a$ and $c$ being coprime integers and $b$ square-free.

What is $a+b+c$ ?

The answer is 26.

1 solution

Ilya Bodo
Dec 9, 2016

The next year that will be a perfect square is 2025. Therefore $\log _{ \sqrt [ 30 ]{ 45 } }{ 2025 } =60$ and $\theta$ =60 degrees. $\frac { 1 }{ 2 } ab\sin { \theta } =area\quad \longrightarrow \quad \frac { 1 }{ 2 } *6*7*\frac { \sqrt { 3 } }{ 2 }$ . This simplifies to $\frac { 21\sqrt { 3 } }{ 2 }$ so a+b+c=21+3+2= $\boxed{26}$

Ugly problem that works out nicely

The answer is 26.

1 solution

0 pending reports