UKMT Senior Challenge-VI

Number Theory Level 2

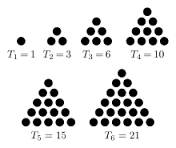How many of the first 2013 triangular numbers are multiples of 5?

This problem is not original.This problem is part of this set .

The answer is 804.

5 solutions

Kalpok Guha
Mar 8, 2015

A triangular number means it is in the form $\frac{n(n+1)}{2}$

Now let $\frac{n(n+1)}{2}=5k$

or $n(n+1)=10k$

$n(n+1)$ must be divisible by $10$

The f values of $n$ are $4,5,9,10,..........,2009,2010$

$5,10,15,............2010$ is a A.P series .Where $2010$ is the $402th$ term.

For each term of the series we have two valuues of $n$

Thus the answer is $2*402=\boxed{804}$

I like your answer. It's more technical. Here is the way I worked on the problems. Hope this give a different perspective (might be the same though). I used the traditional method of finding the sum of the first 100 integers: 50 terms of 101 (1+100, 2+99, etc.).

Short Calculation: 2 terms in every five terms of total 402 terms = 804

Long Explanation

We know that for every five terms, we have two terms divisible by five.

(For example, for the first five terms, fourth term is divisible by five because [2 * 5 (1+4, 2+3) ] = 10 while fifth terms is divisible by five since fourth term + multiple of five yield fifth terms. Apply the same way for every five terms.)

So, within the first 2010 terms, we have 2010/5 = 402 groups of five terms.

In each group, we have 2 terms divisible by five.

So, total we have 804 terms divisible by five within the first 2010 terms.

Since only n4 term and n5 term can be divided by five as explained above, 2011 to 2013 terms are not divisible by 5.

So, final answer is 804 terms.

Shein Phyo - 6 years, 3 months ago

Thank you!your answer is also nice but for every five terms minimum two terms are divisible by not exactly two

Kalpok Guha - 6 years, 3 months ago

Hi, @Kalpok Guha . Can you clarify what you mean by "For every five terms minimum two terms are divisible by not exactly two." What I meant was for every five terms, exactly two terms are divisible by five."

Shein Phyo - 6 years, 2 months ago

It is quite a trivial observation that one of $n,(n+1)$ will be a multiple of $2$ if the other is a multiple of $5$ . So, for the expression to be divisible by $10$ , any one of the terms should be a multiple of $5$ . In short, we'll look for the terms $T_n$ such that $n$ is of the following form:

$n=5p,5q-1~,~1\leq n\leq 2013~,~p,q,n\in \mathbb{Z^+}$

Both the forms produce terms of an AP sequence each with common difference of $5$ for both and as such, the number of terms in each series can be counted easily using AP identities. Both the sequences have $402$ terms each and are disjoint, i.e., there are no common elements among the two sequences. In other words, the intersection of the two sequences is an empty set. Moreover, it is obvious that all the terms of a particular series are also distinct. Thus, we have $402+402=804$ required triangular numbers.

Prasun Biswas - 6 years, 3 months ago

Nice observation

Kalpok Guha - 6 years, 3 months ago

Gamal Sultan
Mar 12, 2015

The general term = n(n + 1)/2 = 5k

n(n + 1) = 10k

Then

n(n + 1) is divisible by 10

Then n must be an element in any of the following sets

(4, 14, 24 , .. , 2004) , (5, 15, 25 , .. , 2005), (9, 19. 29, .. ,2009) , (10, 20, 30, .. , 2010)

Each of the four sets is an arithmetic sequence whose number of terms is 201

So, the answer is 4 X 201 = 804

Hadia Qadir
Aug 30, 2015

The general term = n(n + 1)/2 = 5k n(n + 1) = 10k Then n(n + 1) is divisible by 10 Then n must be an element in any of the following sets (4, 14, 24 , .. , 2004) , (5, 15, 25 , .. , 2005), (9, 19. 29, .. ,2009) , (10, 20, 30, .. , 2010) Each of the four sets is an arithmetic sequence whose number of terms is 201 So, the answer is 4 X 201 = 804

Aran Pasupathy
May 18, 2015

In this arithmetic sequence, the number denoting the position of a particular number(for example, the number denoting the position of 10 is 4) is equal to the number of terms in the sum of terms of the arithmetic progression which starts with 1 and whose common difference is 1.

So if we were to determine the number in the nth position of the arithmetic sequence in this problem, it would be equal to (n/2)[2a+(n-1)d], where a is the first term(1 in this case) and d is the common difference(1 in this case). The formula is therefore n(n-1)/2.

Now we are asked to determine the number of such terms that are multiples of 5. In other words, we are required to solve the equation n(n-1)/2= 5k, where k is an integer.

Multiplying both sides by 2, we get n(n-1)= 10k.

Looking at this equation, we need to find all integers n between 0 and 2013 such that the product of any of those integers and the integer that is one greater than itself is a multiple of 10.

If we look at the first 10 integers, (4x5), (5x6), (9x10) and (10x11) are the only pairs of integers such that the difference between the integers in a pair is 1 and the product of the integers in a pair is a multiple of 10.

This pattern applies to all the remaining sets of 10 integers. Taking the third set of 10 integers, for example, the pairs are (34x35), (35x36), (39x40) and (40x41). Each set of 10 integers contains 4 integers which correspond to triangular numbers that are multiples of 5.

Thus, the number of triangular numbers that are multiples of 5

= (2010/10)x4

= 84

Vincent Miller Moral
Mar 16, 2015

UKMT Senior Challenge-VI

The answer is 804.

5 solutions

0 pending reports