UKMT Senior Challenge-VII
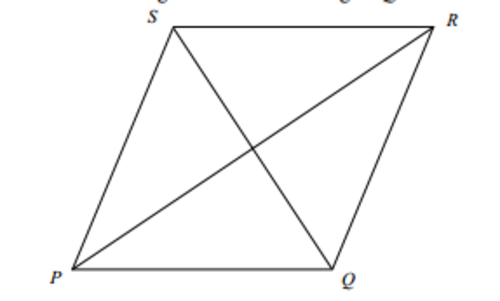 The length of each side of the rhombus PQRS is equal to the geometric mean of the lengths of its diagonals. What is the size in degrees of the obtuse angle PQR?
The length of each side of the rhombus PQRS is equal to the geometric mean of the lengths of its diagonals. What is the size in degrees of the obtuse angle PQR?
This problem is not original.This problem is part of this set .
The answer is 150.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Quite easy one...
We know that area of triangle is 1/2absin(C)
Here, area is a^2/2 (by using the gm property given in the question)
Also area is a^2{sin(S)} getting sin (S)=1/2 and S=150
Moderator note:
Can you add more details to your solution? It's not immediately clear what you are referring to. Is a supposed to be the side of the rhombus? How do you know that the area must be 2 a 2 ?
As the side length 'a' is the geometric mean of diagonals say 'm' & 'n' , So we can say that m n = a S o , m n = a 2 A n d 2 m n = 2 a 2 T h i s g i v e s t h e a r e a o f t h e r h o m b u s . . .
Log in to reply
Thanks for clarifying. Can you edit that into the solution?
Let Q represent the measure of ∠ P Q R (in degrees). The measure of ∠ P S R is 1 8 0 − Q (I'll leave that to you to prove). Let a be the side length of the rhombus. Applying the law of cosines to triangles △ P Q R and △ P S R , I get the equations: d 1 = a 2 + a 2 − 2 a 2 cos ( Q ) and d 2 = a 2 + a 2 − 2 a 2 cos ( 1 8 0 − Q ) . Simplifying... d 1 = a 2 ( 1 − cos Q ) and d 2 = a 2 ( 1 + cos Q ) . Now, applying the condition that the length of the one of the sides of the rhombus is equal to the geometric mean of the lengths of the diagonals, I get a = a 2 ( 1 − cos ( Q ) ) a 2 ( 1 + cos ( Q ) ) ⇒ a 2 = 2 a 2 1 − cos 2 ( Q ) ⇒ 2 1 = sin 2 ( Q ) ⇒ 2 1 = sin ( Q ) . Since Q is obtuse, Q = 1 5 0 ∘ .