Uncertain Mechanics - 2

Classical Mechanics Level 3

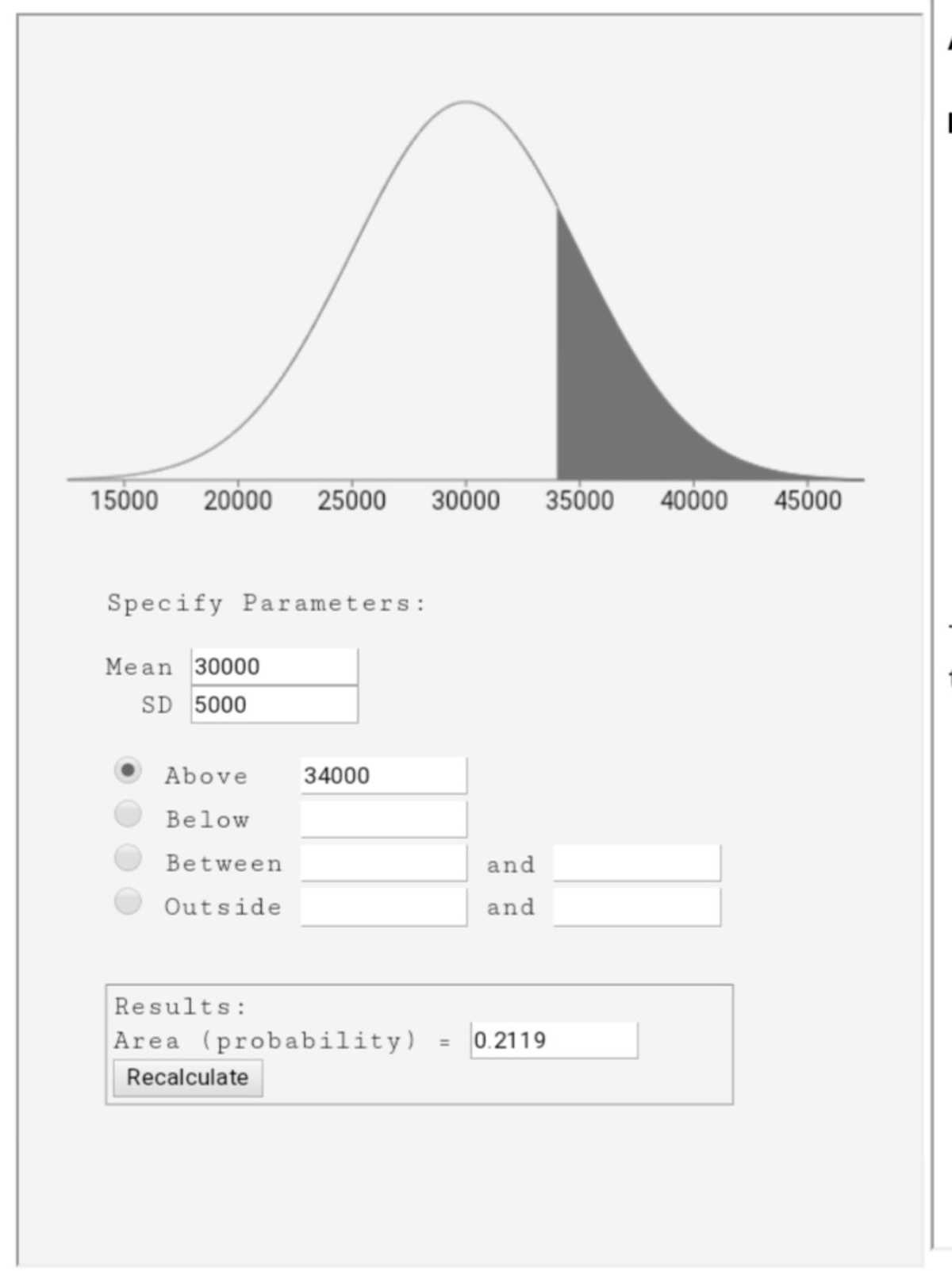
Consider beam A C AC supported at one end A A and at another point B B as indicated on the diagram. Gravity acts downwards and the weight per unit length of the rod is a constant w w . The parameter w w is not exactly known. It is known that it is normally distributed with an expected value of μ = 30000 N / m \mu = 30000 \ N/m and a standard deviation of σ = 5000 N / m \sigma = 5000 \ N/m . It is also known that the support A A cannot withstand a reaction force greater than 8500 N 8500 \ N . If the reaction at A A exceeds the aforementioned value, then the support fails.

Compute the probability of failure of the support at A A .

Note:

  • L = 1 m L= 1 \ m

  • The weight is uniformly distributed throughout the length of the rod.

  • The supports of the rod are indicated by blue circles in the diagram.


The answer is 0.2118554.

Karan Chatrath by Karan Chatrath , 27, Netherlands

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Dark Angel
Jun 29, 2020

3 Helpful 2 Interesting 3 Brilliant 0 Confused

@DARK ANGEL from where you get this calculator?

A Former Brilliant Member - 11 months, 2 weeks ago
Steven Chase
Jun 29, 2020

Comments/explanation are in the attached code 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
 
import math

# Constants

u = 30000.0       # mean
sigma = 5000.0    # standard deviation

Amax = 8500.0     # max withstand force at A
L = 1.0           # Beam length

w1 = u - 6.0*sigma  # min value of w
w2 = u + 6.0*sigma  # max value of w

dw = (w2 - w1)/(10.0**6.0)  # w increment

##########################################

# Sweep w over a range

w = w1

num = 0.0         # Conditional integral of prob density function
denom = 0.0   # Unconditional integral of prob density function (normalizing factor)  

while w <= w2:

    W = w*L        # beam weight

    # W*(L/2.0) = B*(2.0*L/3.0)   # torque balance about A

    B = W*(L/2.0)/(2.0*L/3.0)    # force at B
    A = W - B                    # force at A

    pwr = -0.5*(((w-u)/sigma)**2.0) # gaussian exponent used to calculate PDF (prob density function)
    PDF = math.exp(pwr)*dw   # probability density function

    if A > Amax:
        num = num + PDF*dw   # If support fails, add PDF*dw to num quantity

    denom = denom + PDF*dw   # Always add PDF*dw to denom quantity 

    w = w + dw

##########################################

print (num/denom)
#0.211855977391

2 Helpful 2 Interesting 2 Brilliant 0 Confused

@Steven Chase sir how can we make 2D images in python representing 3D things.
Suggest me some website or video to learn.
Thanks in advance.

A Former Brilliant Member - 11 months, 2 weeks ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...