Under and over

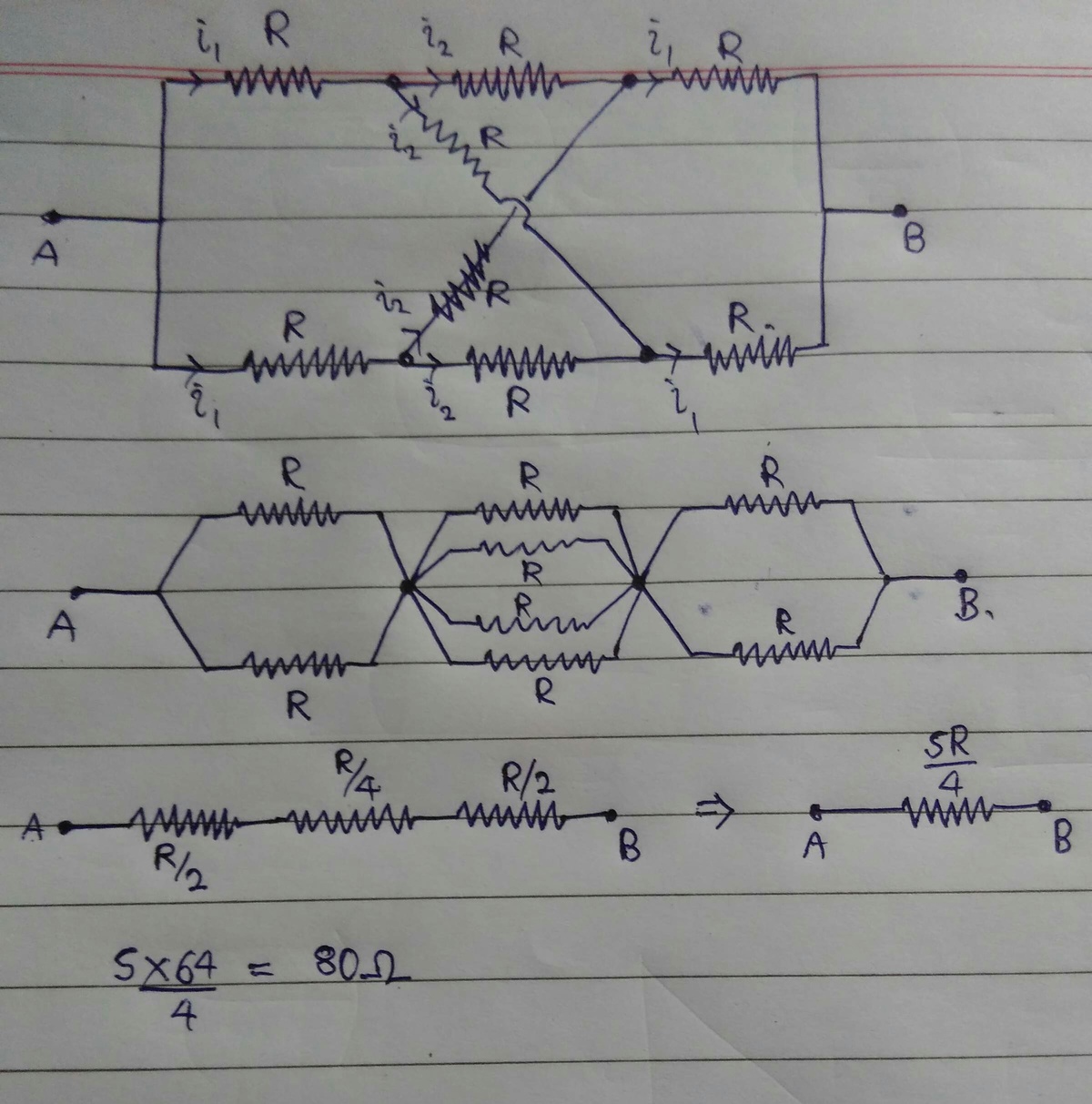In the second step, I have used a shortcut, i.e I used the symmetry of the current in the upper and the lower branch to simplify it to a circuit with fewer equipotential points. I just merged the equipotential points to make the situation easier.

There are two parallel systems which are just the same, so we can find the total resistance of one of them ( $R_{tot1}$ ) and the answer will be its half ( $R_{tot}=\frac{R_{tot1}}{2}$ ). So we have, at one of the systems: $R_{tot1}=2R+\frac{R}{2}$ $\Rightarrow R_{tot}=R+\frac{R}{4}=64+16=80$