Under the cube root

Number Theory Level 4

Find the largest positive integer $x$ such that $x$ is divisible by all the positive integers at most equal to $\sqrt[3]{x}$ .

The answer is 420.

1 solution

John Gilling
May 31, 2015

I figured a a few times wrongly on this one before getting it correct; a very interesting problem that I am still having trouble proving!

For any such $x \in \mathbb{N}$ , we must have that the least common multiple of the set of numbers $\{1, \dots, \left \lfloor{\sqrt[3]{x}}\right \rfloor\}$ , call it $\lambda$ , divides $x$ . Note that $\lambda$ is constant on the intervals between the perfect cube numbers.

After running some pretty convincing numerical results, I found that $\lambda > x$ for $x \geq 8^{3} = 512$ , thus contradicting $\lambda \mid x$ . It would then follow that the interval $[343, 512]$ , where $\lambda = 420$ , would contain our maximum value $x = 420$ .

In order to rigorously prove the numerical claim, I'd like to find a way to describe the growth of $\lambda$ . It is a piecewise constant function of $x$ , with discontinuities at each $x = p^{3n}$ , where $n \in \mathbb{N}$ and $p$ is prime. Below are the graphs of $y = \lambda(x)$ in blue and $y = x$ in red (with logarithmic scaling for both functions on the y-axis).

Domain is $[0,10]$ :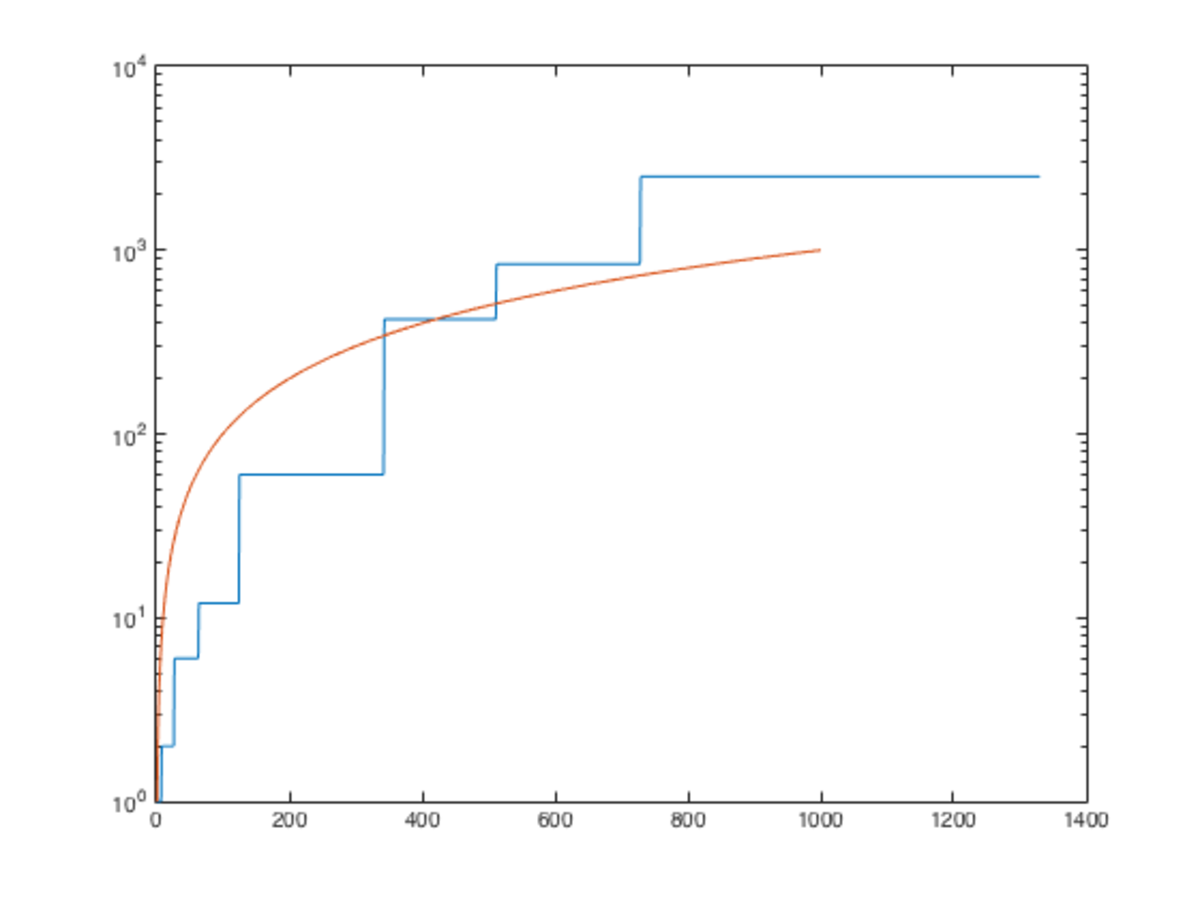

Domain is $[0,20]$ :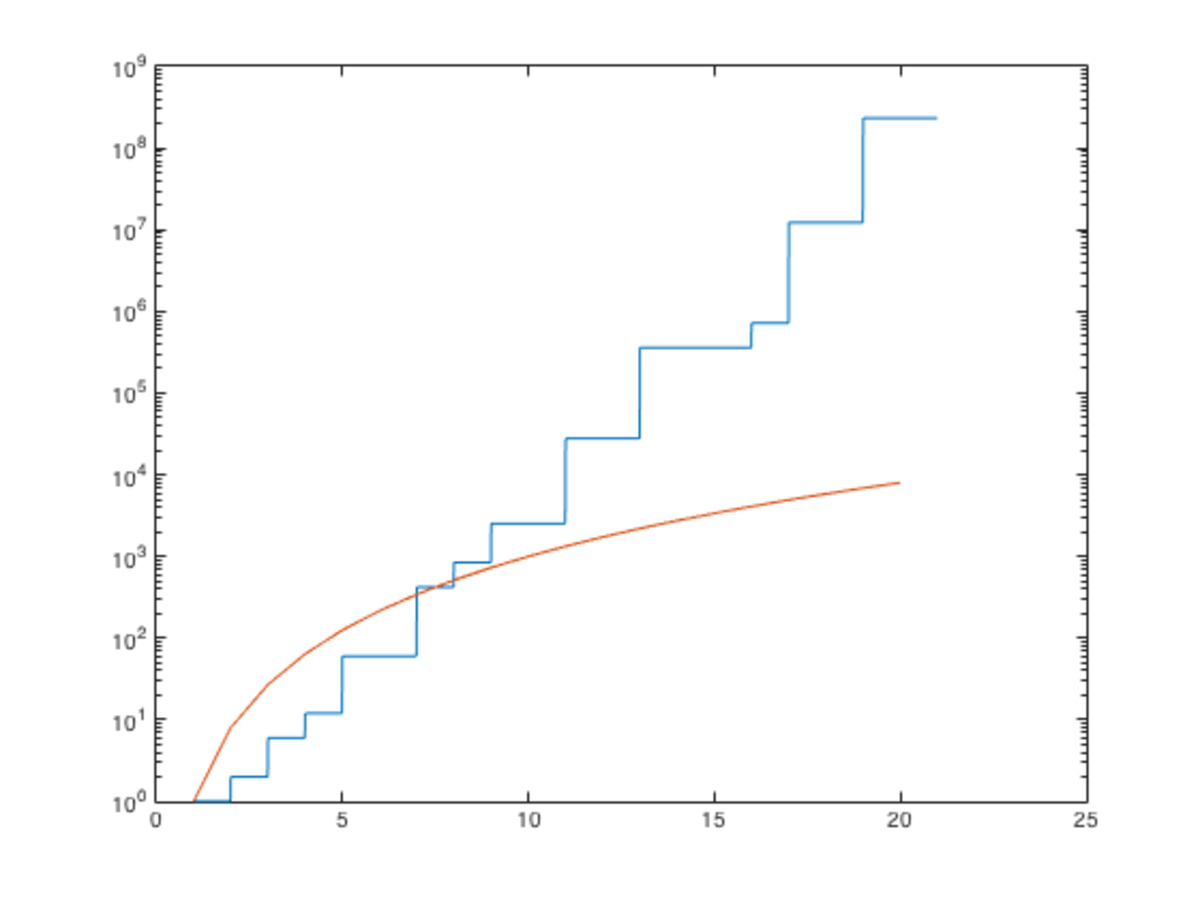

Domain is $[0,50]$ :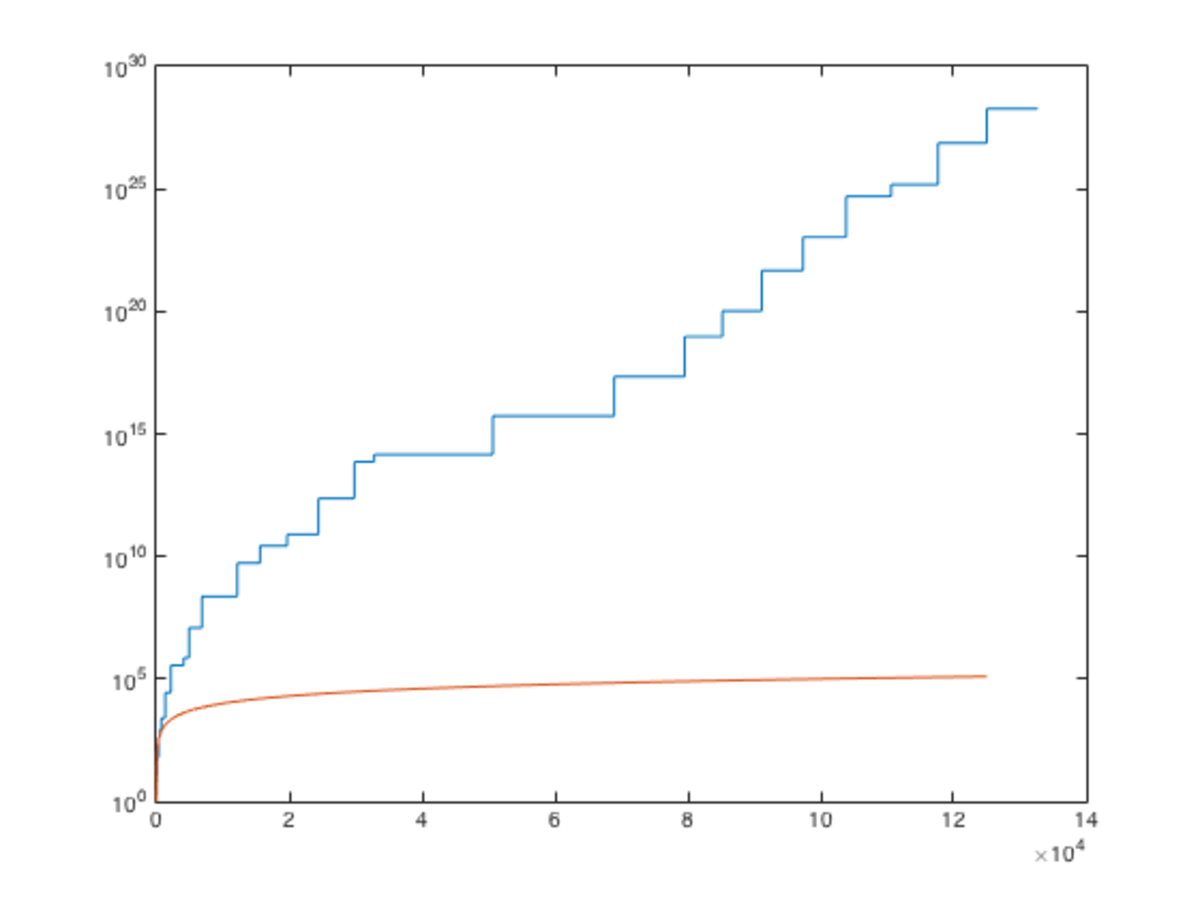

The "accumulated lcm" is apparently growing much quicker than the identity function, but it seems like proving this would have something to do with the distribution of the primes over $\mathbb{N}$ . If someone could give me a gentle hint in the right direction, that would be lovely!

Moderator note:

Let's push your current ideas even further. For clarity, define $\lambda_x = LCM (1, 2, \ldots , \lfloor \sqrt[3]{x} \rfloor )$ .

Suppose there exists an $x \geq 512$ such that $\lambda_x \mid x$ .
Since $x \geq 512$ , this implies that $\lambda_8 \mid x$ , so $840 \mid x$ and thus $x \geq 840$ .
Since $x \geq 840$ , this implies that $\lambda_9 \mid x$ , so $2520 \mid x$ and thus $x \geq 2520$ .
Since $x \geq 2520$ , this implies that $\lambda_{13} \mid x$ , so $360360 \mid x$ and thus $x \geq 360360$ .
We would like for this to continue. For that to happen, we need additional primes, or prime powers, that that will occur in the gap of $\sqrt[3]{2520}$ to $\sqrt[3] { 360360}$ , so on and so forth.

Hint: Bertrand's postulate states that there is a prime number between $n$ and $2n$ .

Under the cube root

The answer is 420.

1 solution

Moderator note:

0 pending reports