Unequal Sisters
Rectangle
A
B
C
D
is divided into three triangles by connecting point
E
on
A
B
to points
C
and
D
.
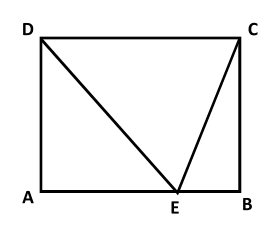
If the triangles A E D , D E C , and E B C are all similar and the ratio of the areas [ E B C ] [ D E C ] = 5 , what is the ratio A B B C ?
If the ratio is in the format b a where a and b are coprime positive integers, report a + b . If you believe that it is impossible to satisfy the above requirements, report your answer as zero.
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Since we work with ratio, let the area of ΔEBC = 1, So BC=2, and EB=1. And AE/AD=2, then AE=2AD = 2BC=4.So AB=5, then BC/AB=2/5. a+b=7
△ D E C is 2 1 of the rectangle, and △ E B C is 1 0 1 so △ A E D is the remaining 1 0 4 .
If the area of △ A E D is 4 times that of △ E B C then its sides are 2 times larger. Specifically A D = 2 × E B .
So also, C B = 2 × E B and we have the ratio of sides of the triangles. A E = 2 × A D = 4 × E B .
The ratio then sought is 4 + 1 2 = 5 2 .
a + b = 2 + 5 = 7
This has to be at E , since the other angles are less than 9 0 ∘ .
The side in △ D E C corresponding to side E B in △ E B C is E C .
If [ E B C ] [ D E C ] = 5 Then E C = 5 E B .
Since we work only with ratios of sizes, we can arbitrarily chose E B = 1 , so that E C = 5 .
Pythagorean theorem results in C B = ( 5 ) 2 − 1 = 5 − 1 = 2 .
E B C B = 2 ⟹ E C D E = 2 ⟹ D E = 2 5
So the hypotenuse of A E D is twice the hypotenuse of A B C , which means A E = 2 × C B = 2 × 2 = 4
A B = A E + E B = 4 + 1 = 5
A B C B = 5 2
2 + 5 = 7