Unfolding Carpet
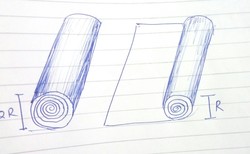 A carpet starts to unfold on a rough horizontal surface.
Calculate velocity of its axis when it's radius becomes half the original one.
A carpet starts to unfold on a rough horizontal surface.
Calculate velocity of its axis when it's radius becomes half the original one.
Details and Assumptions
-
take
-
assume carpet to be perfectly cylindrical.
-
take initial radius to be
The answer is 140.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
It could be easily solved by using conservation of energy. U i + K i = U f + K I
Note that the portion of the carpet that went flat will have no contribution to final potential energy if we take ground as reference line.
Also mass of the new cylinder will be 4 m m g R = 4 m g 2 R + 2 1 4 m v 2 + 2 1 I ω 2 Did you observe that this is the case of pure rolling so , we can say v = 2 R ω
And also by the basics of rotational motion we know that Moment of Inertia of a cylinder is 2 M h 2 about its axis passing through center if the circular faces.
So here it is 2 m ( 2 R ) 2
Plugging in the values and doing some more calculations will take you to v = 3 1 4 g R