Uniform plate of constant areal mass distribution
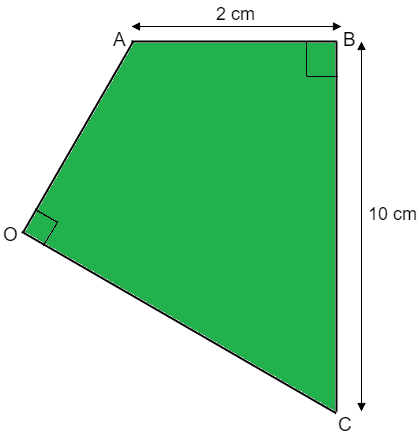 Diagram not to scale
Diagram not to scale
The figure above shows a uniform plate in the shape of a cyclic quadrilateral (with and side lengths and as mentioned). It is given that the sides and are equal.
The mass of the plate is and its moment of inertia perpendicular to the plane of the plate and passing through its vertex can be expressed as , where is a positive constant. Find the value of .
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
There may be a more elegant way to do this, but here's how I did it. I chose to deal with small strips instead of treating the two large triangles as whole entities.
Steps:
1) Divide the plate into two triangles. Side lengths and triangle areas are easily found by inspection (see image).
2) Establish ( x , y ) coordinates for the triangles as shown in the image.
3) Divide each triangle into infinitesimal strips of area d A . Calculate the moment of inertia of each strip using the formula for a rod about its center ( 1 2 M L 2 ) and apply the Parallel Axis theorem to adjust for the distance from the rod's center of mass to point O. Integrate over all strips.
We will need to calculate some angles for use in the Triangle 2 calculations. From Law of Sines (solve by taking asin):
1 0 s i n θ 1 = 1 0 4 1 5 2 s i n θ 2 = 1 0 4 1 θ 3 = 1 8 0 ∘ − θ 1 − θ 2
For Triangle 1
y 1 = 5 2 − x 1 d A 1 = y 1 d x 1 = ( 5 2 − x 1 ) d x 1 d m 1 = A t o t a l d A 1 M t o t a l = A t o t a l M t o t a l ( 5 2 − x 1 ) d x 1
d I 1 = 1 2 d m 1 y 1 2 + d m 1 ( x 1 2 + ( 2 y 1 ) 2 ) = A t o t a l M t o t a l ( 5 2 − x 1 ) [ 1 2 ( 5 2 − x 1 ) 2 + [ x 1 2 + ( 2 5 2 − x 1 ) 2 ] ] d x 1 = A t o t a l M t o t a l [ 3 ( 5 2 − x 1 ) 3 + x 1 2 ( 5 2 − x 1 ) ] d x 1
I_1 = \frac{7}{36}\int_0^\sqrt{52} \Big[\frac{(\sqrt{52} - x_1)^3}{3} +\ x_1^2 (\sqrt{52} - x_1) \Big] dx_1 = \frac{2366}{27}
For Triangle 2
Calculate the horizontal and vertical distances from Point B to Point O.
B O y = 2 + 5 2 c o s θ 3 = 6 B O x = 5 2 s i n θ 3 = 6
y 2 = 2 ( 1 − 1 0 x 2 ) = 2 − 5 x 2 d A 2 = y 2 d x 2 = ( 2 − 5 x 2 ) d x 2 d m 2 = A t o t a l d A 2 M t o t a l = A t o t a l M t o t a l ( 2 − 5 x 2 ) d x 2
d I 2 = 1 2 d m 2 y 2 2 + d m 2 [ ( B O x − x 2 ) 2 + ( B O y − 2 y 2 ) 2 ] = A t o t a l M t o t a l ( 2 − 5 x 2 ) [ 1 2 ( 2 − 5 x 2 ) 2 + [ ( B O x − x 2 ) 2 + ( B O y − 2 2 − 5 x 2 ) 2 ] ] d x 2 = A t o t a l M t o t a l ( 2 − 5 x 2 ) [ 1 2 ( 2 − 5 x 2 ) 2 + ( 6 − x 2 ) 2 + ( 5 + 1 0 x 2 ) 2 ] d x 2
I 2 = 3 6 7 ∫ 0 1 0 ( 2 − 5 x 2 ) [ 1 2 ( 2 − 5 x 2 ) 2 + ( 6 − x 2 ) 2 + ( 5 + 1 0 x 2 ) 2 ] d x 2 = 2 7 2 1 7 0
I 1 + I 2 = 2 7 2 3 6 6 + 2 7 2 1 7 0 = 1 6 8 = 8 4 λ . λ = 2