Unique Equable Isoscles

It's a product of your inspiration problem. As was the result of the discussion there, the unique isosceles triangle is the equilateral triangle for which $\dfrac {4}{A}=\dfrac {1}{3\sqrt 3}$ , where $A$ is the area of the triangle. Hence, from this,

$A=12\sqrt 3$ and the answer is $12+3=\boxed {15}$ .

Let the two equal sides of the isosceles triangle be $y$ and the base be $x$ . Then the perimeter is $P = 2y + x = A$ , which means $y = \frac{1}{2}A - \frac{1}{2}x$ .

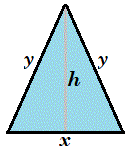
By Pythagorean's theorem, the altitude $h$ of the isosceles triangle from its base is $h = \sqrt{y^2 - (\frac{1}{2}x)^2}$ , so the area is $A = \frac{1}{2}bh = \frac{1}{2}x\sqrt{y^2 - (\frac{1}{2}x)^2}$ .

Substituting $y = \frac{1}{2}A - \frac{1}{2}x$ into $A = \frac{1}{2}x\sqrt{y^2 - (\frac{1}{2}x)^2}$ and rearranging gives $x^3 - \frac{1}{2}Ax^2 + 8A = 0$ .

Since the last term $8A$ is positive and there exists at least one (positive) solution, one root is negative, and since there is only one unique (positive) solution, there must be a double positive root. If $p$ is the double positive root and $-q$ is the negative root, then $(x - p)^2(x + q) = 0$ or $x^3 - (2p - q)x^2 + (p^2 - 2pq)x + p^2q$ . Comparing this to the cubic above, $2p - q = \frac{1}{2}A$ , $(p^2 - 2pq) = 0$ , and $p^2q = 8A$ , which solves to $A = 12\sqrt{3}$ , so that $a = 12$ , $b = 3$ , and $a + b = \boxed{15}$ .