Unit circle triangle problem

Geometry Level pending

A circle has a radius of 1. Two tangents with gradients 2 and -2 meet the circle as shown below. The purple line goes through the diameter and meets one of the tangents on the circumference of the circle.

Find the area of the triangle outlined in red to 3 decimal places.

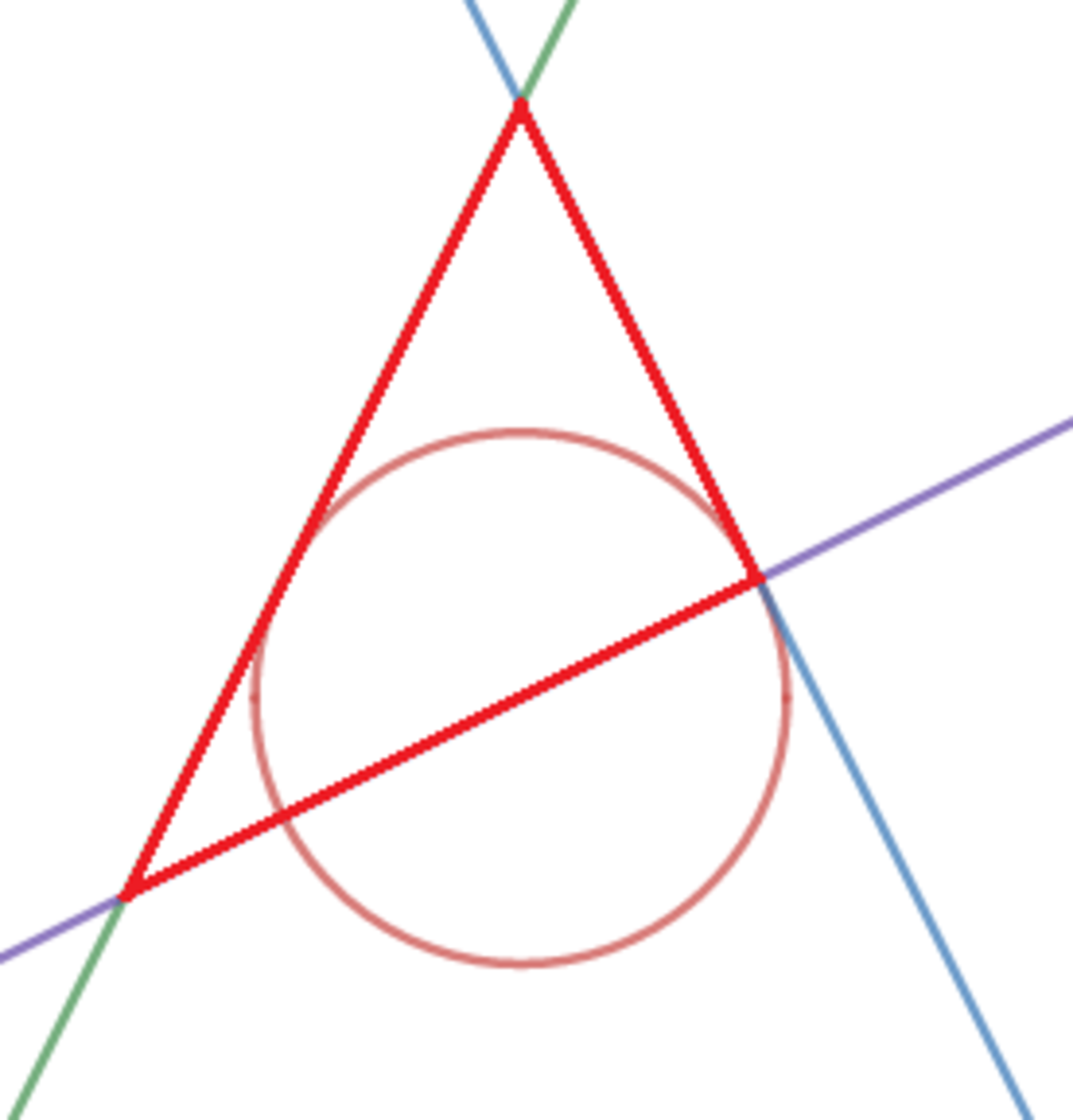
The answer is 2.667.

2 solutions

Bob B
Jan 27, 2017

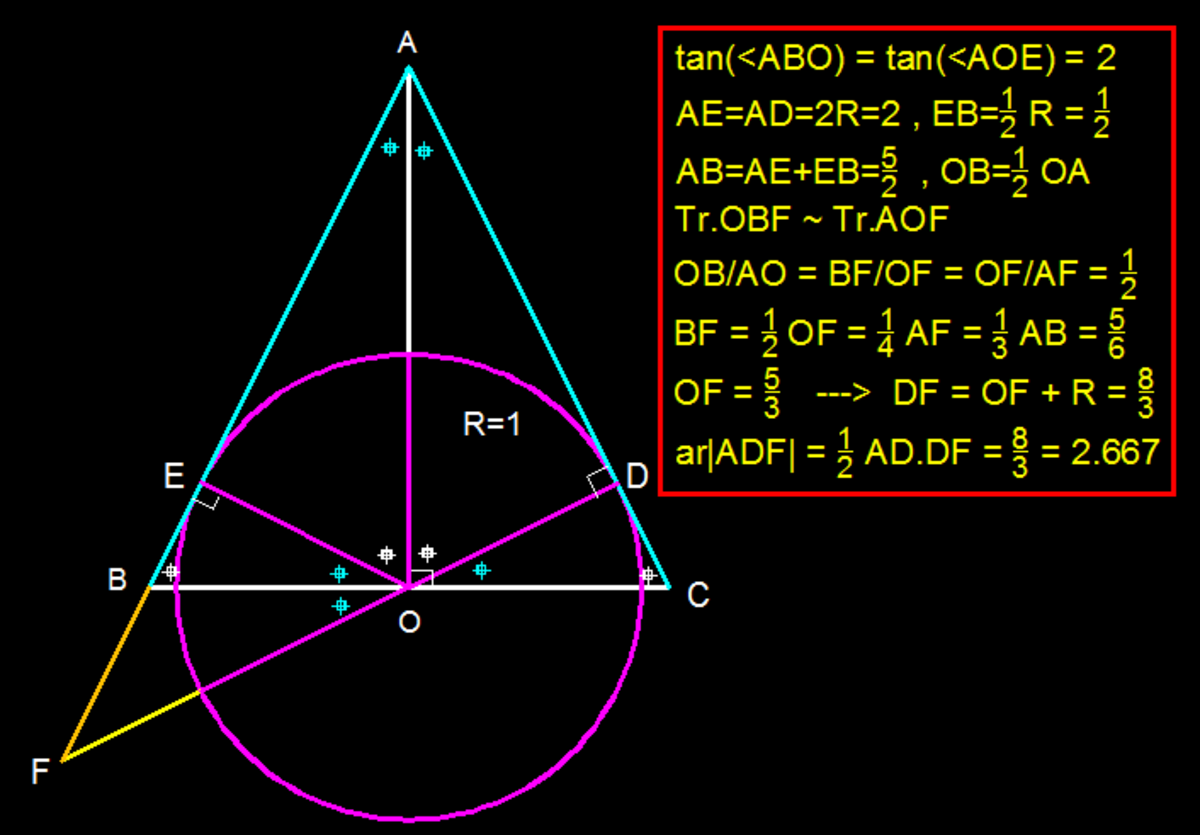
The length of the red part of the blue line is given by $cot(arctan(\frac{1}{2}$ )) $=2$

The angle between the tangents can be found using $180-2arctan(2)$ which is roughly equal to $53.130...$

The red part of the purple line can be given by $2arctan(53.130...)=$ $\frac{8}{3}$

The formula for the area of a triangle $\frac{1}{2}$ $bh$ can then be used to get a result of $\frac{8}{3}$ , which is $2.667$ to 3dp.

The length of the red part of the blue line is given by $cot(arctan(\frac{1}{2}$ )) $=2$

How do you know this? Can you elaborate on this?

Pi Han Goh - 4 years, 4 months ago

A lot of people are aware that a point on the circumference of a unit circle can be used to find the cosine/sine of the angle between the line connecting the centre and the horizontal axis, i.e. the height of the point on the circumference from the centre is the sine of the angle and the cosine of the angle is the width of the point on the circumference to the centre, however a lot of people are unaware of a similar method for tangents and cotangents of the angle.

The tangent is given by the length of the tangent from the point of intersection on the circumference to the intercept point on the horizontal axis, and the cotangent is given by the length of the tangent from the point of intersection on the circumference to the intercept on the horizontal axis.

As for the working to get the length of the red part of the blue tangent, the purple line is perpendicular due to it effectively being the point where a tangent meets a radius, so if we imagine the circle being in the centre of a coordinate plane, the purple line has gradient 0.5, i.e. y=(1/2) x. We can then work out the angle by using tan(theta)=o/a. We get theta=arctan((1/2) x/x), which cancels out to arctan(1/2). Then, using the cotangent method stated above we can say the length of the red part of the line cot(theta), which is therefore equal to cot(arctan(1/2)). Using the identity cot(x)=(tan(x))^-1, we can see that it is given by 1/(tan(arctan(1/2))), which cancels out to 1/(1/2)=2.

I hope my explanation was satisfactory.

Bob B - 4 years, 4 months ago

Ahmad Saad
Feb 11, 2017

Unit circle triangle problem

The answer is 2.667.

2 solutions

0 pending reports