Unit Cubes 1 – Counting Faces
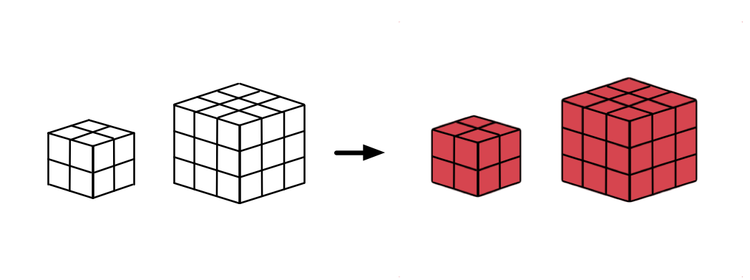 Consider the outside of cubes made out of
unit blocks, with side lengths
, for
, which we have painted red on the outside.
Consider the outside of cubes made out of
unit blocks, with side lengths
, for
, which we have painted red on the outside.
The following table shows the number of unit cubes which are colored on a given number of faces.
| Cube Size | 3 faces red | 2 faces red | 1 face red |
| 8 | 0 | 0 | |
| 8 | 12 | 6 | |
| ? | ? | ? |
What is the sum of the numbers missing from the row for the cube?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4x4x4 cube has 64 cubes total to build it, with a 2x2x2 cube of 8 small cubes on the inside. Since we aren't asked the individual pieces, but the sum, the question really is how many are painted with at least one side.
Thus, 64-8 = 56 "painted" cubes.