Unit Spheres in N dimensions

The surface $S_N$ of a sphere of radius $r$ in $N$ dimensions is given by $S_N = \Omega(N) r^{N-1}$ , where $\Omega(N) = \frac{2\pi^{\frac{N}{2}}}{\Gamma(\frac{N}{2})}$ is the solid angle in $N$ dimensions. $\Omega(N)$ is therefore the surface of an $N$ dimensional unit sphere. Since the Euler Gamma function $\Gamma(N)$ grows to infinity faster than any exponential (as a matter of fact $\Gamma(n) = (n-1)!$ for any integer $n$ ), we easily obtain that $\lim_{N \rightarrow \infty} \Omega_N = 0$ , which means that $\Omega(N)$ have at least one local maximum in $(0,\infty)$ . Evaluating numerically $\frac{d\Omega}{dN}=0$ yields $N_{max} \simeq 7.257$ , which approximated to the closest integer is 7.

i am going to derive the formula for surface area of a nth dimension sphere. but if we were to recursively integrate to find the surface area, we would have to integrate with respect to $ds$ , which would be messy. so instead first the volume is going to be found. notice that the volume would be $V(n,r)= f_n r^n$ , so we are only going to find $f_n$ and add on the radius part later. we start of by the equation $x_1^2+x_2^2+....+x_{n-1}^2+x_n^2=1\to x_1^2+x_2^2+....+x_{n-1}^2=\sqrt{1-x_n^2}^2$ which implies that a nth dimensional sphere can be thought of as multiple (n-1) dimensional sphere with radius of the form $\sqrt{1-x_n^2}$ from 1 to -1. or that $f_{n+1} = \int_{-1}^1 V(n,\sqrt{1-x_n^2}) dx_n= f_{n} \int_{-1}^1 (1-x_n^2)^{n/2} dx_n$ we just need to find $\int_{-1}^1 (1-x_n^2)^{n/2} dx_n = 2 \int_0^1 (1-x_n^2)^{n/2} dx_n=^{:u=x_n^2} \int_0^1 u^{-1/2} (1-u)^{n/2} du =\beta(1/2, n/2+1)\\= \dfrac{\sqrt{\pi} \Gamma(n/2+1)}{\Gamma((n+1)/2+1)}$ now obviously using recursion: $f_{n+1}=\dfrac{\sqrt{\pi} \Gamma(n/2+1)}{\Gamma((n+1)/2+1)} f_n = \dfrac{\sqrt{\pi} \Gamma(n/2+1)}{\Gamma((n+1)/2+1)}\dfrac{\sqrt{\pi} \Gamma((n-1)/2+1)}{\Gamma(n/2+1)} f_{n-1}\\=\dfrac{\sqrt{\pi} \Gamma(n/2+1)}{\Gamma((n+1)/2+1)}\dfrac{\sqrt{\pi} \Gamma((n-1)/2+1)}{\Gamma(n/2+1)}.....\dfrac{\sqrt{\pi}\Gamma(1)}{\Gamma(1/2+1)} f_1$ notice the telescope. we are left with (using $f_1=2$ ) $f_{n+1} = \dfrac{2(\sqrt{\pi})^{n+1}}{\Gamma((n+1)/2+1)}\to f_n= \dfrac{2(\sqrt{\pi})^n}{\Gamma(n/2+1)}$ so we have $V(n,r)= \dfrac{2(\sqrt{\pi})^n}{\Gamma(n/2+1)}r^n \to S(n.r) = \dfrac{\partial V(n,r)}{\partial r} = \dfrac{2n(\sqrt{\pi})^n}{\Gamma(n/2+1)}r^{n-1}$ so for a unit nth sphere $S_n = \dfrac{2n(\sqrt{\pi})^n}{\Gamma(n/2+1)}$ . it cannot be maximized analytically ,at least to the best of my skills so i graphed it. 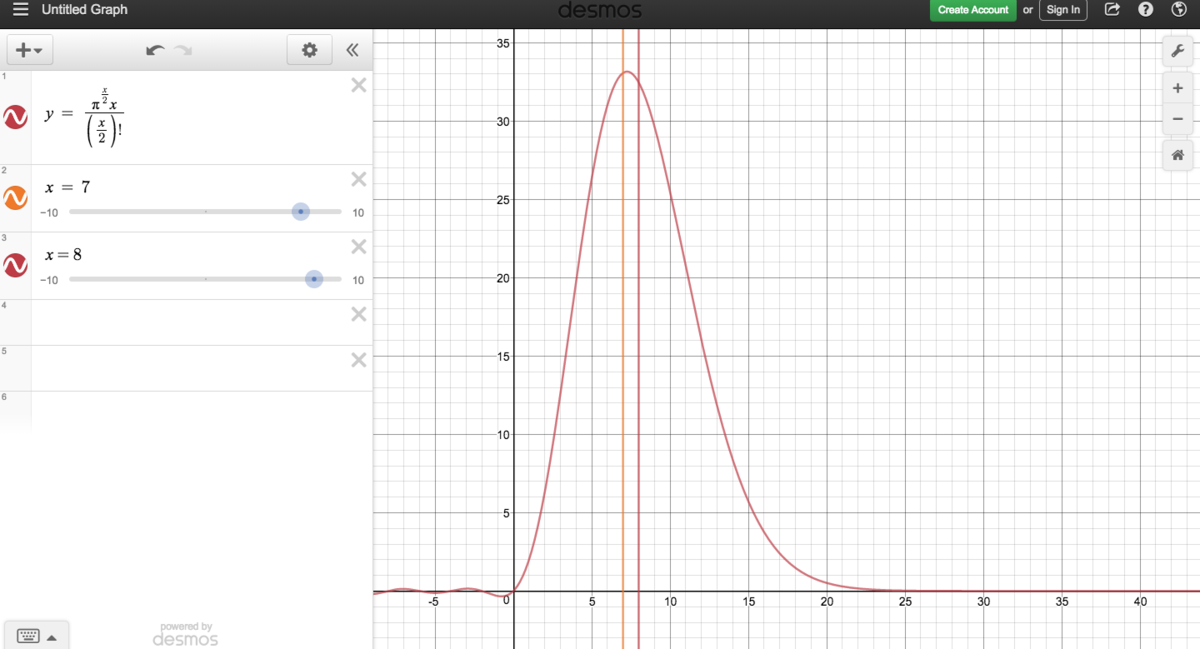it can be seen that among the two contenders of 7 and 8, 7 yields a higher answer, so the number of dimensions that would maximize the surface area of an unit NTHsphere is $\boxed{7}$