Unity-Gain Phase Shifting Transformer

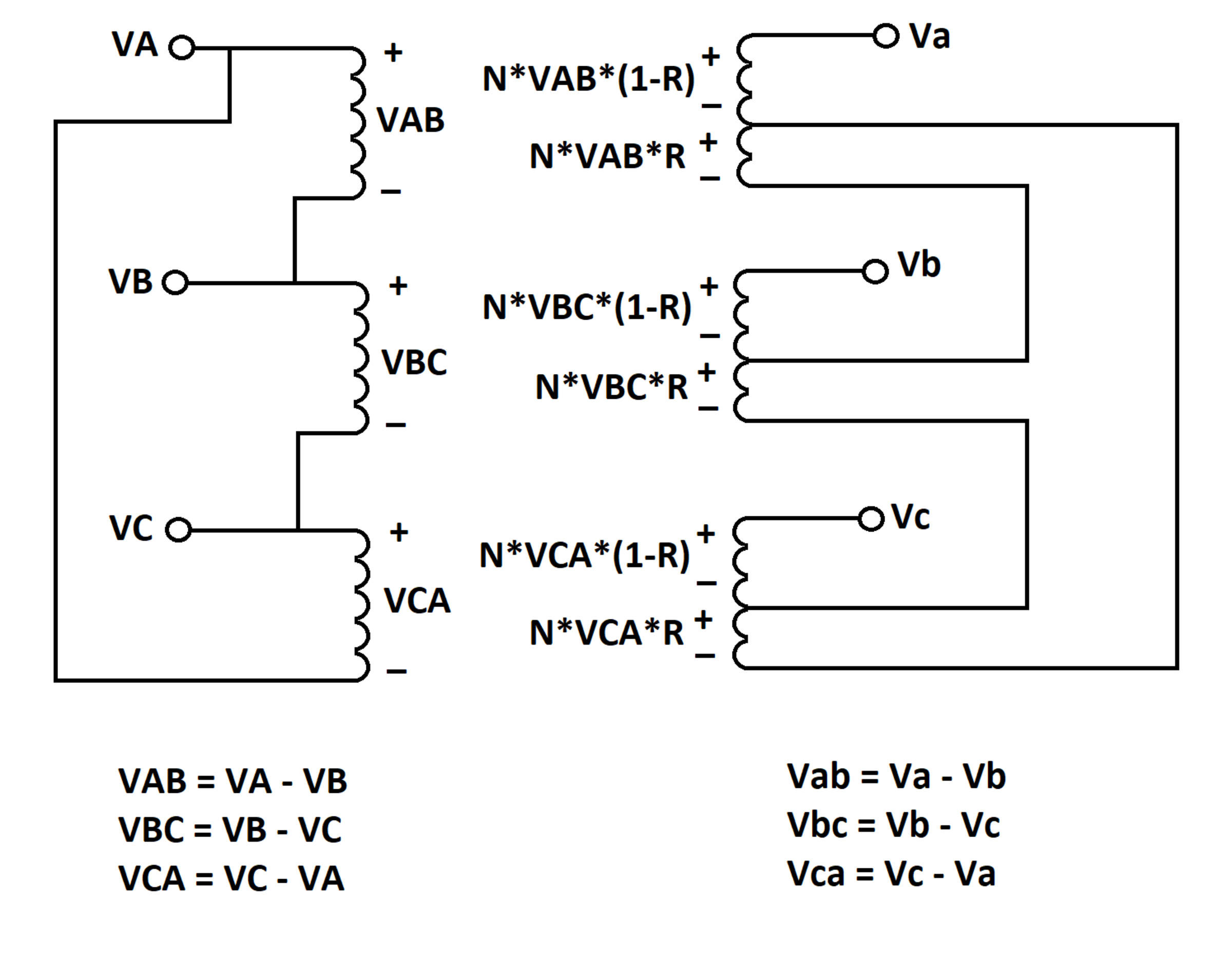
Electricity and Magnetism Level pending

A three-phase AC transformer is connected in a delta configuration on the left side. The winding voltages on the left side are:

V A B = V A − V B = e j 0 V B C = V B − V C = e − j 2 π / 3 V C A = V C − V A = e j 2 π / 3 V_{AB} = V_A - V_B = e^{j 0} \\ V_{BC} = V_B - V_C = e^{-j 2 \pi/3} \\ V_{CA} = V_C - V_A = e^{j 2 \pi/3}

The transformer has a turns ratio of N N , resulting in voltages N V A B N V_{AB} , N V B C N V_{BC} , and N V C A N V_{CA} across the windings on the right side. Each coil on the right side is divided into two sub-windings as shown in the diagram, with R R being the ratio of the number of turns in the lower sub-winding to the total number of winding turns. The sub-winding voltages are proportional in the same way, and these are explicitly given in the diagram. The lower winding portions on the right are connected in a delta configuration.

Determine the values of N N and R R such that the phase-to-phase voltage on the right side has the same magnitude as that on the left side, and leads by a phase angle of π / 12 \pi / 12 .

V a − V b V A − V B = V a b V A B = e j π / 12 \frac{V_a - V_b}{V_A - V_B} = \frac{V_{ab}}{V_{AB}} = e^{j \pi / 12}

Enter your answer as N + R N + R .

Details and Assumptions:
1) The winding fraction R R must be a real number between 0 0 and 1 1 .
2) Transformer turns ratio N N must be a positive real number
3) e e is Euler's number, and j j is the imaginary unit


The answer is 1.4505.

Steven Chase by Steven Chase , 37, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Karan Chatrath
May 22, 2021

The line indicated in the diagram is grounded. This implies that:

V a − 0 = N ( 1 − R ) V A B V_a - 0 = N(1-R)V_{AB} 0 − V 2 = N R V A B 0 - V_2 = NRV_{AB} V b − V 2 = N V B C ( 1 − R ) V_b - V_2 = NV_{BC}(1-R)

It is given that V A B = 1 V_{AB} = 1 . Therefore:

V a − 0 = N ( 1 − R ) V_a - 0 = N(1-R) V b = N V B C ( 1 − R ) + V 2 V_b = NV_{BC}(1-R) + V_2 V b = N V B C ( 1 − R ) − N R V_b = NV_{BC}(1-R) -NR

Therefore:

V a − V b V A B = V a − V b = N ( 1 − R ) − N V B C ( 1 − R ) + N R \frac{V_a - V_b}{V_{AB}} = V_a - V_b = N(1-R)-NV_{BC}(1-R) +NR V a − V b = cos ⁡ ( π 12 ) + j sin ⁡ ( π 12 ) = N − N ( 1 − R ) ( − 1 2 − j 3 2 ) V_a - V_b = \cos\left(\frac{\pi}{12}\right) + j \sin\left(\frac{\pi}{12}\right) = N - N(1-R)\left(-\frac{1}{2} - j \frac{\sqrt{3}}{2}\right) ⟹ cos ⁡ ( π 12 ) + j sin ⁡ ( π 12 ) = ( 3 N 2 − N R 2 ) + j ( 3 N 2 − 3 N R 2 ) \implies \cos\left(\frac{\pi}{12}\right) + j \sin\left(\frac{\pi}{12}\right) = \left(\frac{3N}{2} - \frac{NR}{2}\right) + j \left(\frac{\sqrt{3}N}{2} - \frac{\sqrt{3}NR}{2}\right)

Equating the real and imaginary parts allows us to solve for N N and R R .

N = cos ⁡ ( π 12 ) 3 − sin ⁡ ( π 12 ) 3 N = \frac{\cos\left(\frac{\pi}{12}\right)\sqrt{3} - \sin\left(\frac{\pi}{12}\right)}{\sqrt{3}} R = 3 N 2 − sin ⁡ ( π 12 ) 3 N 2 R =\frac{ \frac{\sqrt{3}N}{2} - \sin\left(\frac{\pi}{12}\right)}{ \frac{\sqrt{3}N}{2}}

N + R = 1.4505 N + R = 1.4505

3 Helpful 3 Interesting 3 Brilliant 0 Confused

Nice solution

Talulah Riley - 3 weeks ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...