Unknown sides, known area
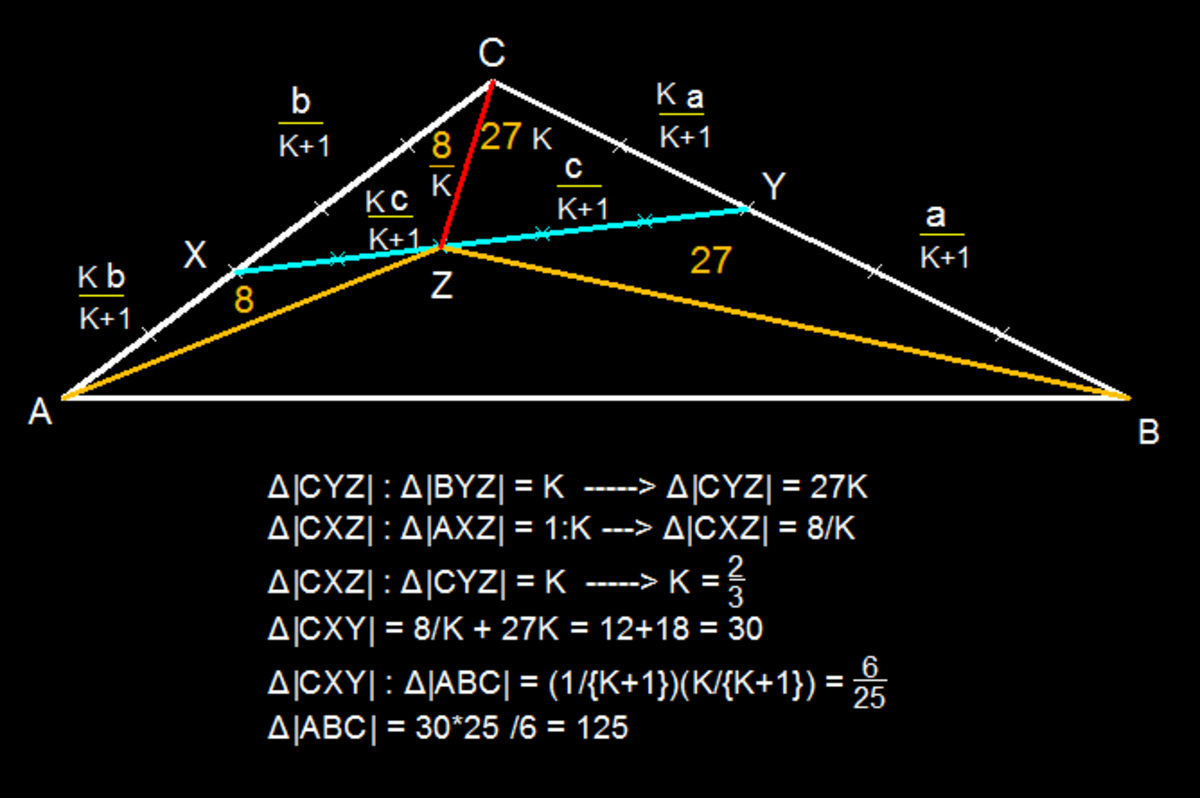
Consider a triangle A B C with points X and Y located on sides A C and B C which divide the said segments at equal proportions. That is, X C A X = Y B C Y = k . Locate a point Z along X Y that shall also divide it in the same manner that points X and Y divide A C and B C , respectively. That is, Z Y X Z = k as well.
If the area of Δ Z A X = 8 and the area of Δ Z Y B = 2 7 , find the area of Δ A B C .
The answer is 125.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
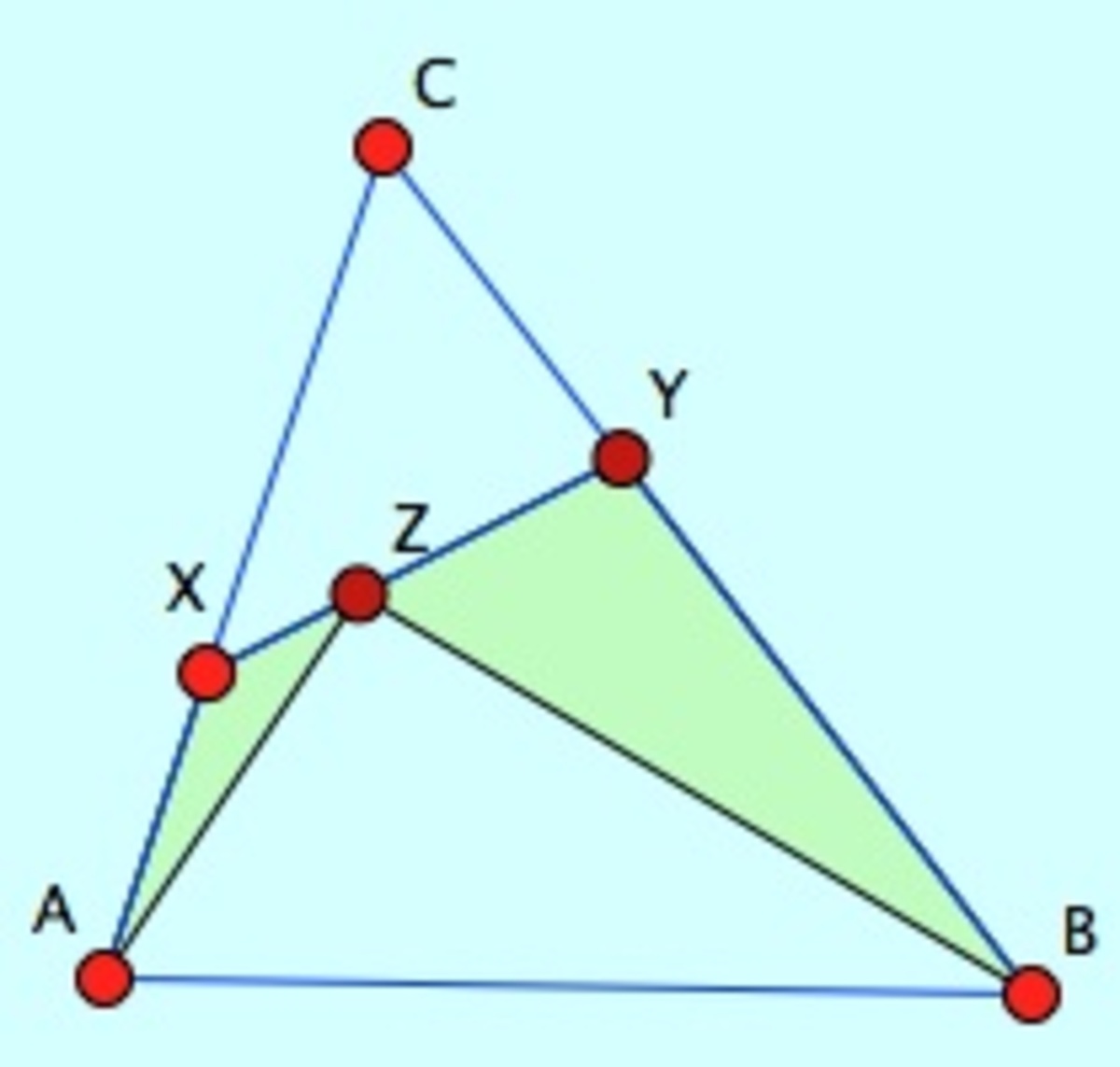
Let the ratio within the segments be k .
Now, we can see that A Δ A Y C = k A Δ A B C , as if we were to treat this side as the base, with the height unchanged, a shift in the base length with some ratio will also result to the same shift in area.
In a similar manner, we can see that A Δ A Y X = k A Δ A Y C , which in turn implies that A Δ A Y X = k 2 A Δ A B C . Then, once again, we will find that A Δ A Z X = k A Δ A Y X , implying finally that A Δ A Z X = k 3 A Δ A B C . We will use this later.
We can also start at Δ B X C , proceed to Δ B X Y , then to Δ B Z Y . We will eventually arrive at A Δ B Z Y = ( 1 − k ) 3 A Δ A B C .
Now, observe that
( A Δ Z A X ) 3 1 = k ( A Δ A B C ) 3 1
( A Δ B Z Y ) 3 1 = ( 1 − k ) ( A Δ A B C ) 3 1
adding them all, we get
A Δ Z A X ) 3 1 + ( A Δ B Z Y ) 3 1 = ( A Δ A B C ) 3 1
and cubing both sides, we arrive at
( A Δ Z A X ) 3 1 + ( A Δ B Z Y ) 3 1 ) 3 = ( A Δ A B C )
and so we can now find the area of Δ A B C , and that is
( 8 3 1 + 2 7 3 1 ) 3
( 2 + 3 ) 3
5 3 = 1 2 5