Unusual Inscribed Circle 1
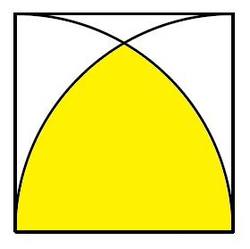The figure shown is a square with quarter circles drawn from two adjacent corners. If the side of the square is 10, find the radius of the largest circle that can be inscribed in the area of the yellow region.
The answer is 3.75.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Imgur
Elegant solution Sir! I solved the same way, just adding the figure here Pythagoras in triangle ACB - 5 2 + r 2 = ( 1 0 − r ) 2 2 5 + r 2 = 1 0 0 − 2 0 r + r 2 2 0 r = 7 5 r = 3.75
Log in to reply
Just saw it ! I did not get any intimation ? Any way it is nice short simple solution, as your solution always are.
Log in to reply
Thank you Sir! I had not come to Brilliant for several months. Got an email about another problem I had reported long time back. But glad to be back and read your message!
Exactly same way!!
Nice solution, I did it a more geometric way.
Because there is only one inscribe-able circle, it will occur when there is an upside down equilateral triangle inscribed in the yellow region
same way...
\text { Let the radius of the required circle be R & center}~ O_R, \text{ the center of the} \\ \text{ right quarter circle be } O_Q \text{ and the point of tangential contact be T (also} \\ \text{ on the right). Let M be the midpoint of the base side of the square. } \\~\\ \text{ Radius of quarter circle }=10=O_QT\text { is the straight line containing two} \\ \text{ collinear radii and } O_Q O_R \text{ touches the arc of the yellow area at T.} \\\therefore10= O_QT = O_Q O_R + O_R~T = O_Q O_R+R \Longrightarrow O_Q O_R = 10-R~~..(1)\\In~the ~right~angled~~\triangle~O_RMO_Q~~....O_RM^2+M O_R^2 = O_Q O_R^2\\\Longrightarrow R^2+5^2=O_Q O_R^2.....(2)\\ By`(1) and~(2)~\therefore~( 10-R)^2=R^2+5^2 \Longrightarrow~ on ~solving~~R=3.75. \\~\\\boxed{3.75}