Up, up and away

Look at any three successive people in the line. Let $A,B,C$ be the tops of their heads in sequence, and let $D,E,F$ be the bottoms of their respective feet. Let the horizontal line through $A$ intersect $BE$ at $P$ , and let the horizontal line through $B$ intersect $CF$ at $Q$ . Then $\Delta APB$ and $\Delta BQC$ are similar, and so

$\dfrac{|CF|}{|BE|} = \dfrac{|CF|}{|BQ|} = \dfrac{|CQ| + |QF|}{|BQ|} = \dfrac{|CQ|}{|BQ|} + 1 = \dfrac{|BP|}{|AP|} + 1 = \dfrac{|BP| + |AP|}{|AP|} = \dfrac{|BE|}{|AP|}.$

Thus the heights of any three successive people are in geometric progression, and thus the heights of all $2015$ people are in geometric progression.

Now the height $h_{n}$ of the $n$ th person is given by the formula $h_{n} = h_{1}r^{n-1}$ for some real number $r \gt 1.$ We are given that $h_{1} = 49$ inches and $h_{2015} = 81$ inches, so

$81 = 49r^{2014} \Longrightarrow r = (\dfrac{81}{49})^{\frac{1}{2014}}$ ,

and thus $h_{1008} = 49*[(\dfrac{81}{49})^{\frac{1}{2014}}]^{(1008 - 1)} = 49\sqrt{\dfrac{81}{49}} = 49*\dfrac{9}{7} = \boxed{63}$ inches.

Let the positions of the 2015 people be $x_0, x_1, \cdots, x_{2014}$ , and their heights be $y_0, \cdots, y_{2014}$ . By hypothesis, it follows that $y_0 = 49$ , $y_k = x_{k+1} - x_k$ for $k = 0, \cdots, 2013$ , and $y_{2014} = 81$ . Further, the $(x_i, y_i)$ 's satisfy a linear equation of the form $y_i = mx_i + b$ for $i = 0, \cdots, 2014$ . Without loss of generality, we may assume $x_0 = 0$ , so that $b = 49$ . In particular, we find the sequence $(x_k)_{k \geq 0}$ satisfies the recursion $x_{k+1} = (m+1)x_k + 49.$ Define the generating function $f(z) = \sum_{k=0}^\infty x_k z^k.$ Then, the recursion implies the generating functional equation $f(z) \left(\frac{1 - (m+1)z}{z}\right) = \frac{49}{1-z}.$ Solving this equation, we find that $f(z) = \frac{49}{m} \left(\frac{1}{1 - (m+1)z} - \frac{1}{1-z}\right).$ Extracting coefficients, we see that $x_k = \frac{49}{m}\left((m+1)^k - 1\right)$ for $k = 0, 1, \cdots, 2014$ . Now, we substitute $y_{2014} = 81$ to obtain $81 = \frac{49}{m}\left((m+1)^{2014} - 1\right)m + 49,$ which implies that $(m+1)^{1012} = \frac{9}{7}.$ The height of the middle person is given by $y_{1012} = \frac{49}{m}\left((m+1)^{1012} - 1\right)m + 49,$ which after simplification becomes $y_{1012} = 49 (m+1)^{1012} = 63.$

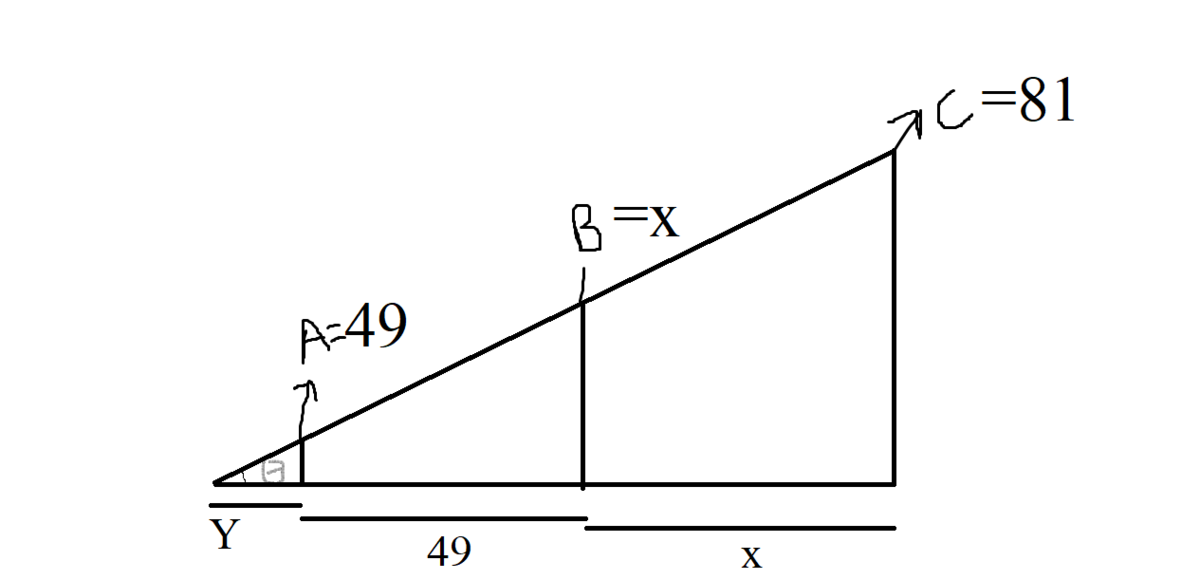
• Here it doesn't matter how many people are standing in the line given the height of the smallest and the tallest and the heads are are collinear.
• So now using the above figure we can make 3 simple equations which are shown below:

• Now equating the values from the above equations we get the following: