Upside-Down Triangles

To turn a three-story pyramid of coins ( with 1 + 2 + 3 = 6 coins ) upside down, we only need to move 2 coins: moving the bottom left and bottom right coins next to the top coin.
Now, what if there are 1 + 2 + 3 + ⋯ + 1 0 0 = 5 0 5 0 coins instead? What is the minimum number of coins we have to move in order to turn this huge, 100-story pyramid upside down?
Bonus: Generalize this for a pyramid of 1 + 2 + 3 + ⋯ + n coins.
The answer is 1683.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Playing devil's advocate, I (mostly) agree that if we make the assumption that the untouched coins have a parallel grid structure, then we would want an (almost) regular hexagon in the middle. (The somewhat easier way to do this, is to do the calculus calculation each time we move the pyramid down/left/right by 1.)
However, I do not yet see an obvious reason why the grids must be parallel (or even of the same unit length).
Log in to reply
That doubt has occurred at the back of my mind. I still feel confident that the maximal set of untouched coins has to be the arrangement that comes closest to a regular hexagon, but I will think about this and try to find an explicit argument.
OK, I've more rigorously defined the "turn-upside-down" operation as a bijection between two well-defined sets of lattice points in Z 3 . A vector, or "coin", is said to be unmoved if and only if the function maps it onto itself. The "overlap" between the "right-side-up-triangle" set and the "up-side-down-triangle" set is simply their intersection, or the set of all vectors in the first set that the "turn-upside-down" function maps onto themselves. There are an infinite number of "turn-upside-down" functions, but "most" of them don't produce any "overlap". We are interested in studying the functions that do produce an overlap, and determining what is the maximum order of the overlap set for a given triangle and its image, and the structure of that set. I'm betting that I can show that when two vectors are "unmoved", then all the vectors "in between" them must also be unmoved, and that the overlap is greatest when it is centered at the center of the triangle.
Wouldn't The answer be n-1? To achieve this answer keep the two central coins in the base of the pyramid. Move the rest n-2 coins along with the top coin. Move the top coin to the bottom along the central line of the pyramid. Now move the remaining (n-2) coins to the 2nd rank (from the top previously) and place them symmetrically. Actually you did the same thing . The difference Just crops up because we are dealing with discrete (and not continuos) distribution of materials.
Log in to reply
That would work for n = 4 , but by n = 6 , you already have to move n + 1 coins. Think about it this way: the rows directly above the bottom row are also going to be much too wide to remain untouched. In every case, the minimum number you have to move is the closest integer to exactly one-third of the total number of coins in the pyramid.
The new triangle is obtained by point-reflection of the old triangle. We take a small triangle a rows from the top ( triangle 1 ) and move them, upside down, to the bottom of the triangle. Immediately above them, we can leave a + 1 coins from the bottom row in place. In this bottom row, there are b coins to the left and c coins to the right that will have to be moved. They form the bases of two other small triangles ( triangle 2 and triangle 3 ) that will be moved.
The number of coins in each small triangle is 2 1 x ( x + 1 ) , where x is the size of that triangle. Thus we have { a + b + c = N − 1 2 1 a ( a + 1 ) + 2 1 b ( b + 1 ) + 2 1 c ( c + 1 ) = K here, K is the number of coins to be moved. This number must be minimized. We do this by considering the total derivative of K : d K = ( a + 2 1 ) d a + ( b + 2 1 ) d b + ( c + 2 1 ) d c . Writing c = N − 1 − a − b we have d c = − ( d a + d b ) , so that d K = ( 2 a + b + 1 − N ) d a + ( a + 2 b + 1 − N ) d b . a and b can now be varied independently. To minimize K , both of their coefficients must therefore be zero: { 2 a + b + 1 − N = 0 a + 2 b + 1 − N = 0 Subtracting gives a = b , and substitution shows a = b = c = 3 1 ( N − 1 ) .
In this case, N = 1 0 0 so that a = b = c = 3 3 ; and we find K = 3 ⋅ 2 1 ⋅ 3 3 ⋅ 3 4 = 1 7 × 9 9 = 1 6 8 3 .
Generalization
If N is not one more than a multiple of 3, it is not possible to have a = b = c = 3 1 ( N − 1 ) because they must be integers. Instead, we make a = ⌊ 3 1 ( N − 1 ) ⌋ , c = ⌈ 3 1 ( N − 1 ) ⌉ , and b equal to either a or c . K = { 6 1 ( N − 1 ) ( N + 2 ) 6 1 N ( N + 1 ) N ≡ 1 mod 3 N ≡ 0 , 2 mod 3
Finally, consider that the total number of coins is A = 2 1 N ( N + 1 ) ; thus we see that K = { 3 A − 1 3 A N ≡ 1 mod 3 N ≡ 0 , 2 mod 3 or simply K = ⌊ 3 A ⌋ .
Let the flipped and unflipped pyramids be F and U respectively.
Let Uk denote the row of U containing k coins etc. If we wish to maximise the number of points in common between F and U, then we must superimpose F on U, meaning that Fn must coincide with Uk for some well chosen k, Fn-1 with Uk+1, and so on.
Let us define the shift operation as follows: If Fn coincides with Uk, then applying the operation once makes Fn coincide with Uk+1, Fn-1 with Uk+2 and so on.
Let us begin with coinciding Fn and U1 etc. F1 will then have one point in common with Un. F2 will have two points in common with Un-1 and so on until Fk has all points in common Un-k-1. Clearly Fk+1,Fk+2,...,Fn will have all points in common with Un-k-2,..., U1 respectively.
What about the remainder?
At Un we have n-1 remaining, at Un-1 we have (n-1)- 2 = n-3 remaining, at U(n-2) we have n-5 remaining and so on.
So the remainder in the unshifted case is a pyramid of odds or evens up to (n-1) (evens if n odd, odds if n even), call this remainder pyramid R.
What is the effect of shifting by one row?
U1 becomes part of the remainder and we subtract one from each of the rows of R.
If we shift by k rows, U1, U2,...,Uk become part of the remainder, forming their own remainder pyramid S, and we subtract 1 from each row of R for each shift ie. subtracting k from each row and discarding negatives.
There is a clear net loss in remainder as long as the number of rows in the remainder pyramid is greater than the number of points in Uk+1 where we have shifted by k rows.
Now note that R has n/2 rows for n even, (n-1)/2 rows for n odd. (Check this by examining Un). Further note that two shifts reduce the number of rows of R by one.
Thus (for n even) we want to find the largest integer k such that:
Even number of shifts: n/2 -k >= 2k Odd number of shifts: n/2 -k -1 >= 2k+1
The number of rows of S will be 2k or 2k+1 and the corresponding number of rows of R will be n/2 -k or n/2 -k-1 respectively.
This number of coins in S will equal the sum of integers up to 2k or 2k+1, and the number of coins in R will equal the sum of odds up to (n/2 -k)th term or the sum of evens up to (n/2 -k-1)th term.
The smaller of the two is our desired answer. In the case of n=100, we have: K=16 in both cases, 32 shifts: 0.5(32x33) (S) + 34^2 (R) = 1684
33 shifts: 0.5(33x34) (S) + 2x0.5(33x34) (R) = 1683
(Note the sum of odds up to nth term is the nth square number and the sum of evens up to nth tern is twice the sum of integers up to nth term)
The same analysis can be repeated for the odd case noting that with no shifts R is a pyramid of evens as opposed to odds.
(Apologies for the wordiness, I cannot seem to figure out how to illustrate or typeset my answers)
Isn't this all overly complicated? Above a certain size, the pyramid in question can be flipped by moving 1/3 of the coins, as in 5050/3=1683.33. Round off. Problem solved!
Intuitively, it makes sense that, at the minimum, you will need to move one-third of the pyramid to turn it upside down. (See figure below)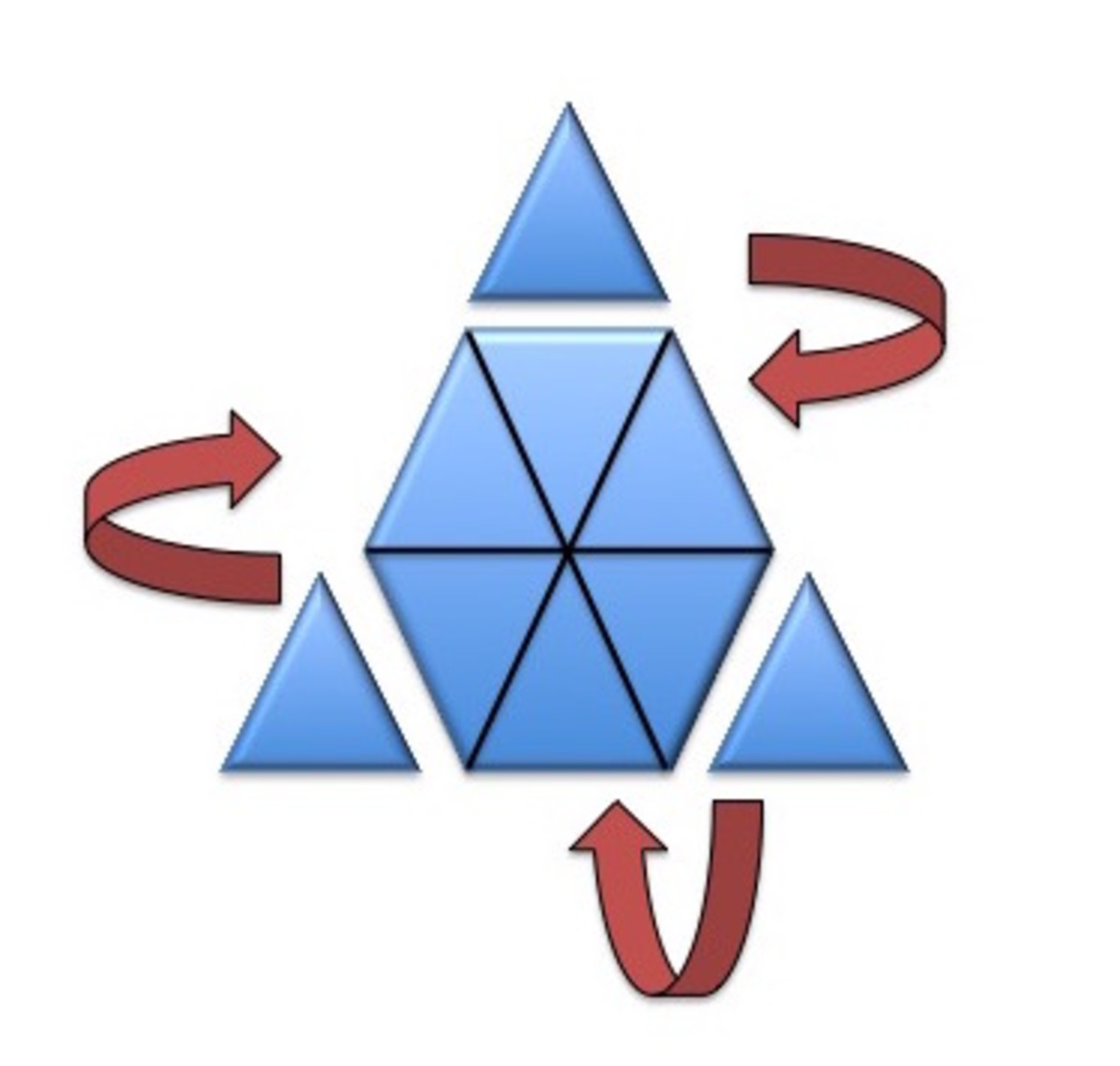 In fact, if
m
represents the minimum number of coins that need to be moved in order to do this, then
m
=
⌊
6
n
(
n
+
1
)
⌋
, meaning the integer part of exactly one-third of the number of coins in the pyramid,
2
n
(
n
+
1
)
. Substituting
n
=
1
0
0
, we get
m
=
1
6
8
3
In fact, if
m
represents the minimum number of coins that need to be moved in order to do this, then
m
=
⌊
6
n
(
n
+
1
)
⌋
, meaning the integer part of exactly one-third of the number of coins in the pyramid,
2
n
(
n
+
1
)
. Substituting
n
=
1
0
0
, we get
m
=
1
6
8
3
How can we demonstrate this? (Note: the demonstration below is still rough, and I will be working on making it clearer and tighter.) First, we need to think about what the part of the pyramid that will not need to be moved looks like. It will have to have the reflective symmetry of a rhombus. The figures below show the possibilities for the pyramid n = 9 . The green dots represent unmoved coins; the red dots coins that have to be moved.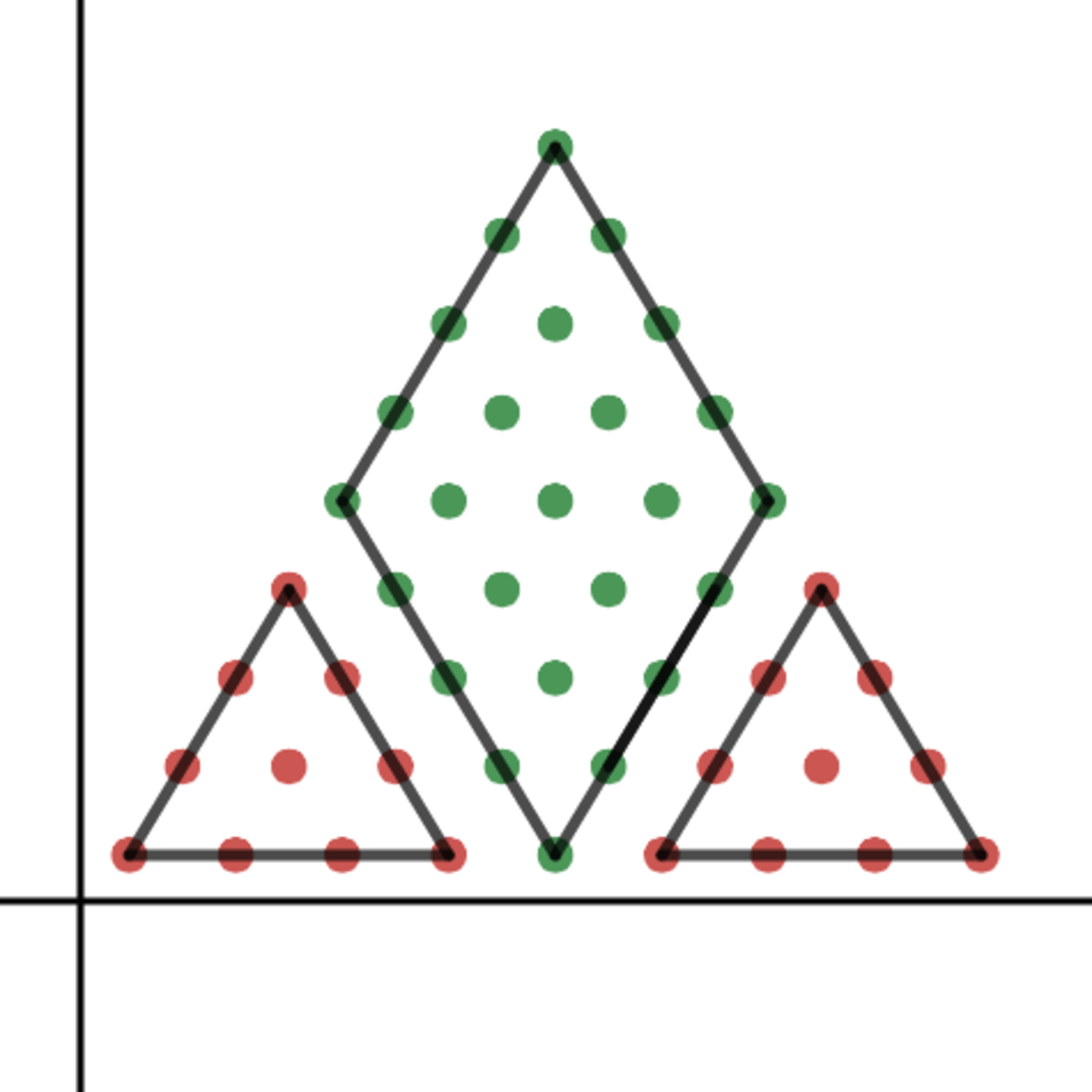
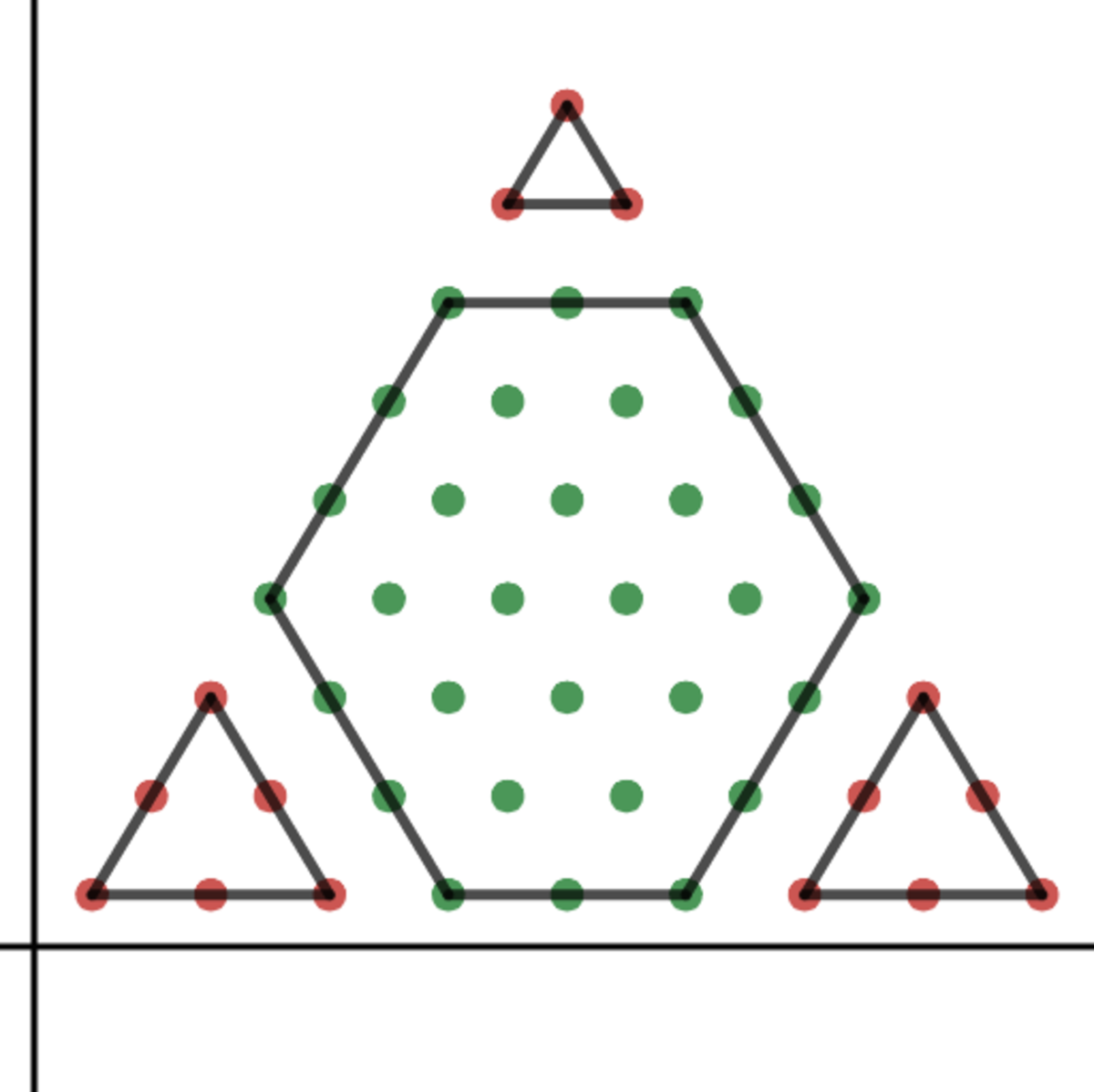
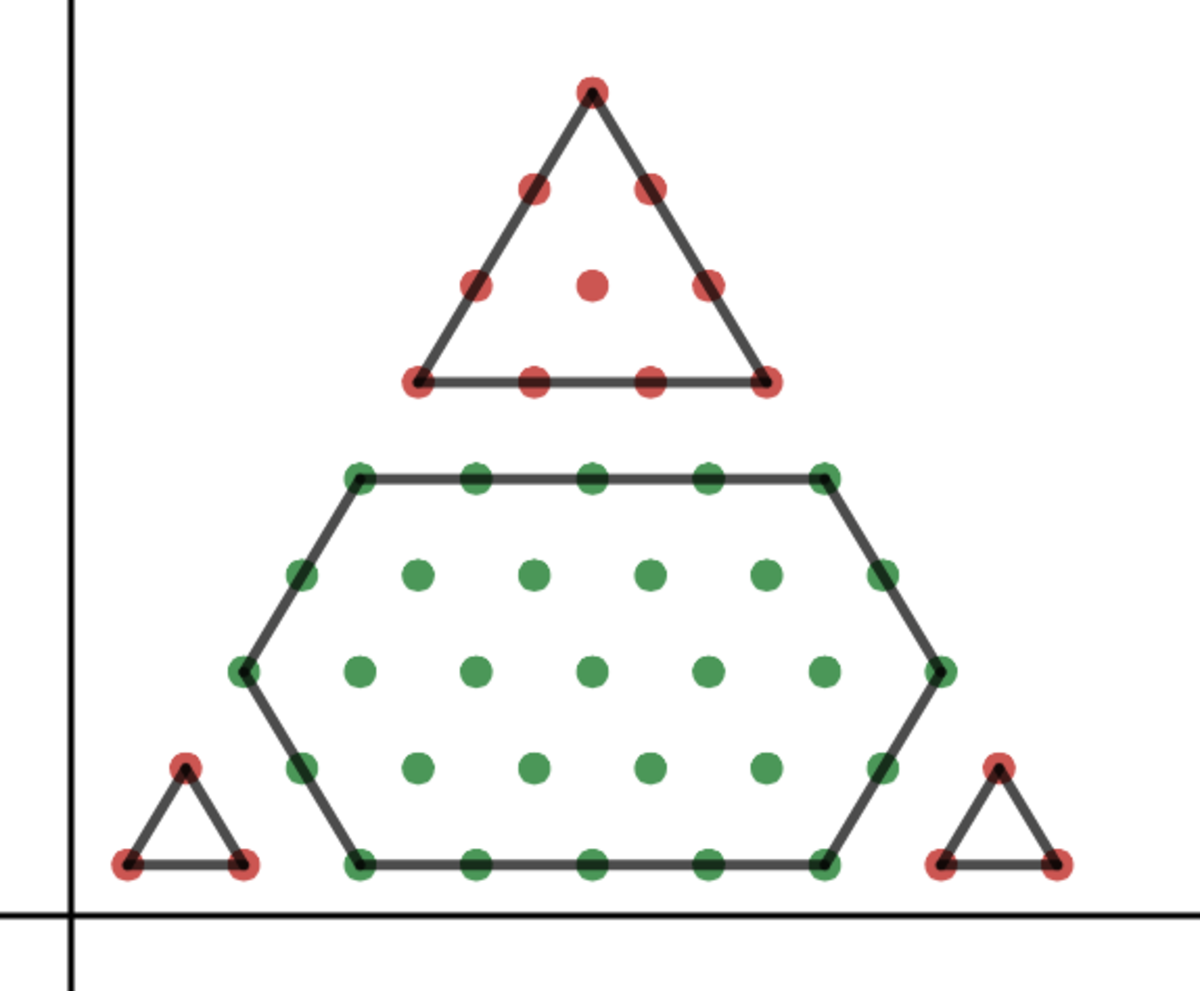
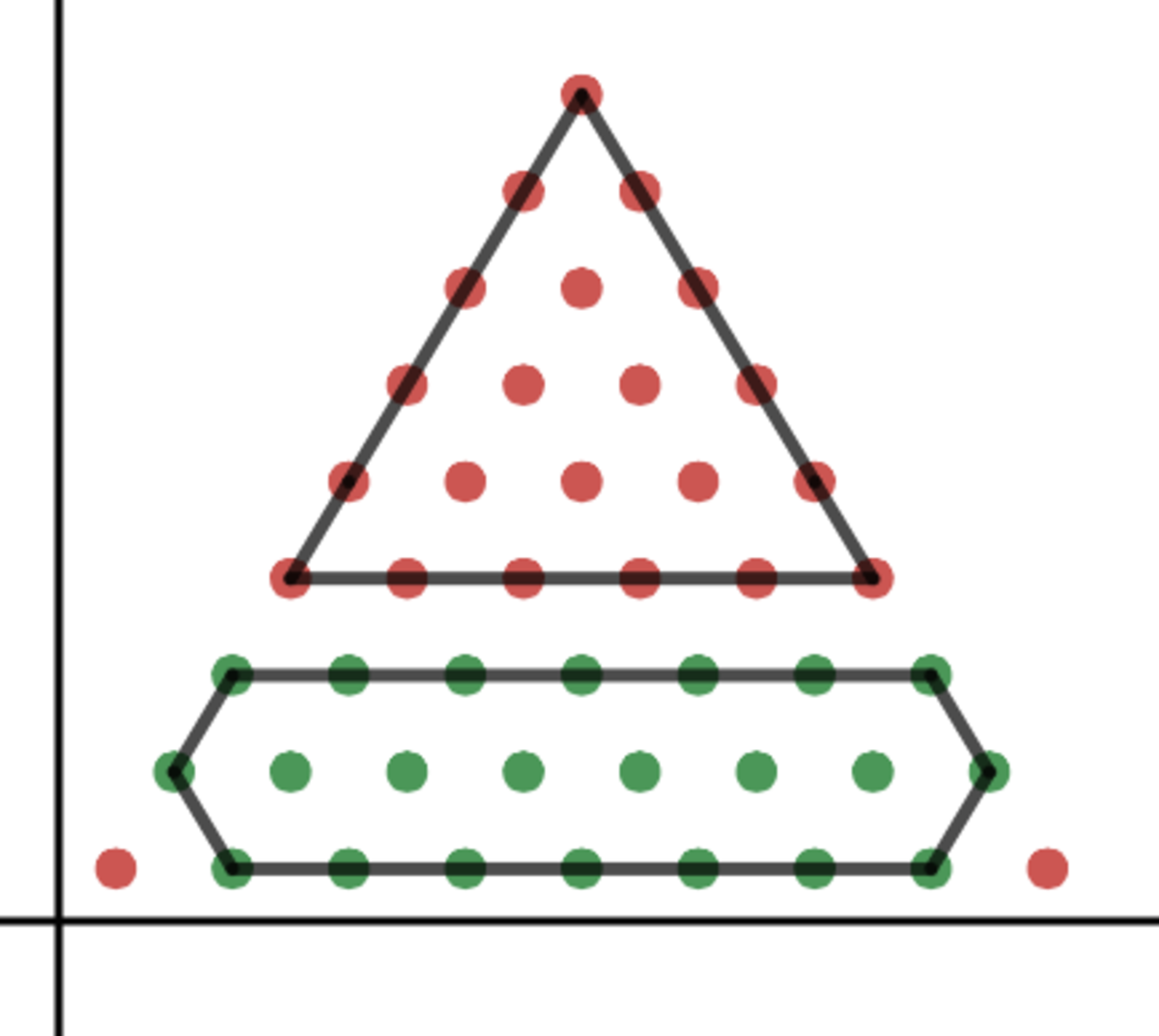
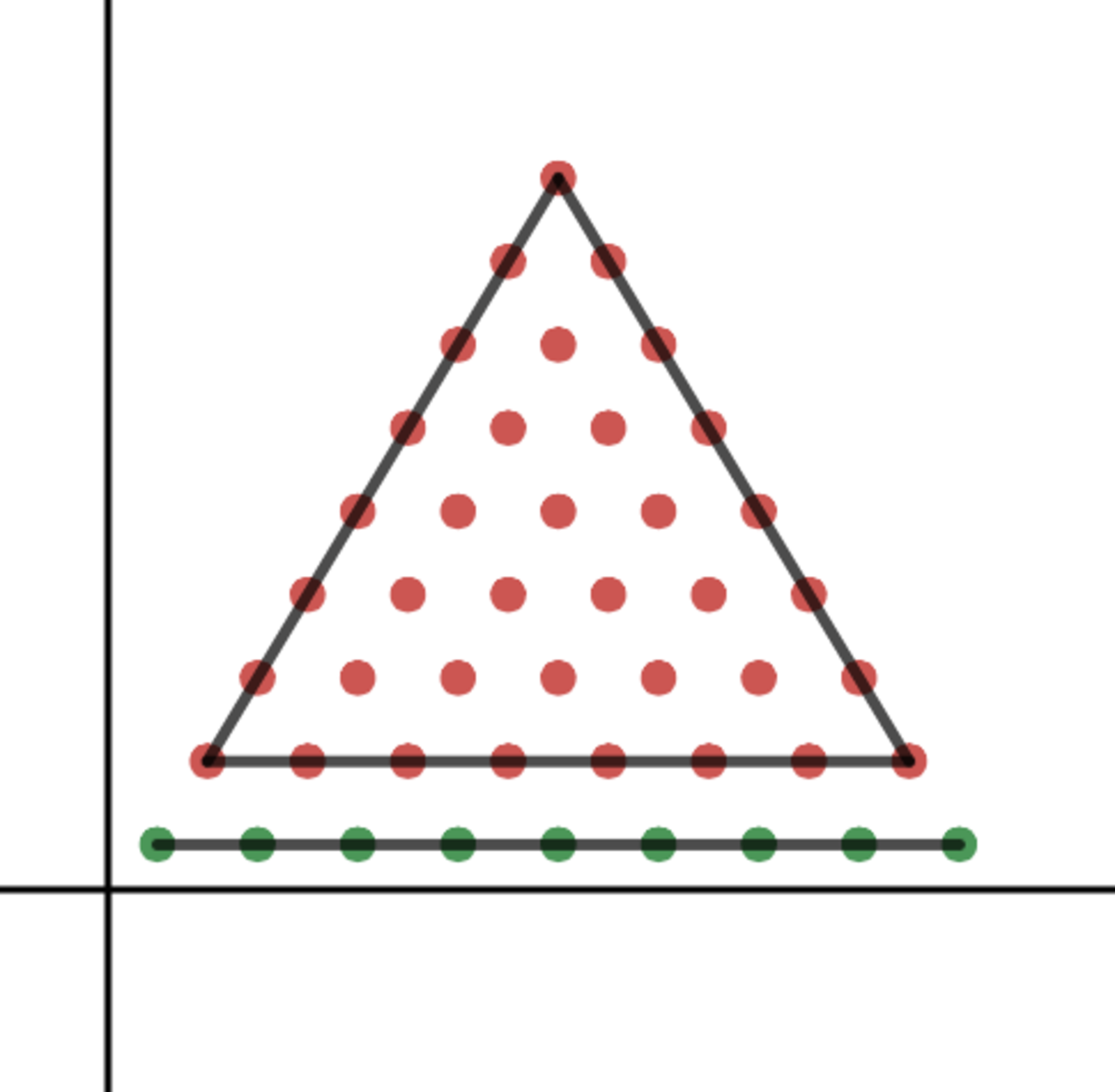
Clearly, we want to choose the green figure that minimizes the number of red dots. One way of doing this is to find a general formula for the green areas, and then optimize. We notice that the figures are all truncated rhombi. Let u represent the number of unmoved coins (green dots), and let r represent the row of the triangle on which the truncated rhombus starts. Then we can derive the formula u = 4 ( n + r ) 2 − r ( r − 1 )
This formula represents chopping off two smaller triangles from a larger rhombus. It can be simplified as u = 4 − 3 r 2 + 2 r ( n + 2 ) + n 2
Holding n constant, and differentiating by r , we find that there is a maximum where r = 3 n + 2 . The problem is that this does not always yield an integer. Not only must r be an integer, since it is a row index of the triangle, it must also have the same parity as n , to preserve symmetry. Let n be represented by one of the three classes 3 p − 2 , 3 p − 1 , or 3 p . The table below shows the possibilities:
For example, I read across the third row. If n is even, and n = 3 p − 1 , then p = 3 n + 1 , so p must be odd. Substituting 3 p − 1 for n in 3 n + 2 , we find that the maximum is where r = p + 3 1 . However, the closest even integer (the only legal value in this case) to p + 3 1 is p + 1 , so it is this value of r , which I call r 0 , that will maximize u . From the table, it turns out that the value of r 0 does not depend on whether n is odd or even. We can fill in the appropriate value of r 0 into our formula, and get a value for u , the maximum number of unmoved coins. Call the total number of coins in the pyramid t . We can express t in terms of p , and then subtract our value for u to get the minimum number of coins that need to be removed, m . The table below brings all this together.
The last column shows that the minimum number of coins that have to be moved in order to turn the pyramid upside down is exactly equal to the integer part of exactly one-third of the total number of coins in the pyramid, as I stated at the beginning.