UR grid
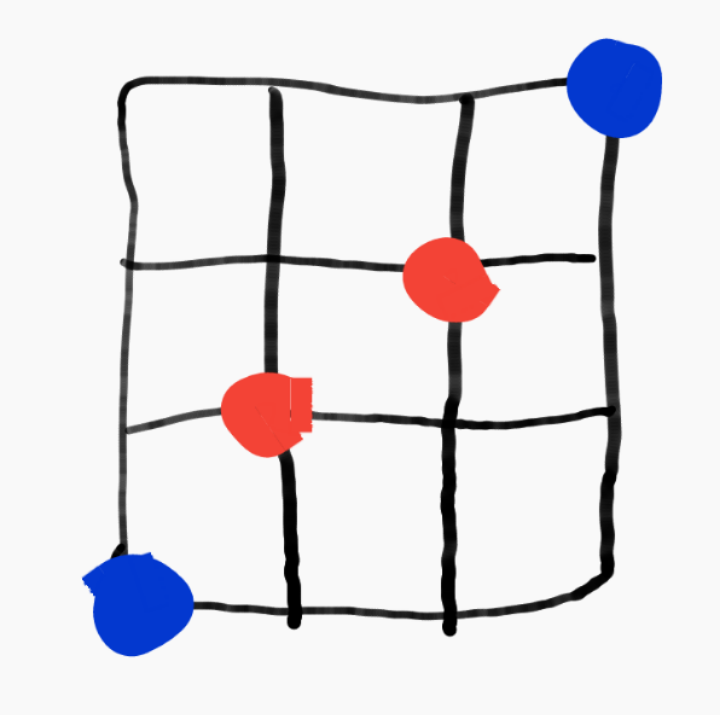
In how many ways you can go from the point to the point ,only going and , at most passing through one red dot .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
I will solve using "The complementary method",
The number of all ways to go from ( 0 , 0 ) to ( 3 , 3 ) is ( 3 6 ) = 2 0 ,
We have to subtract the ways that passes throught the two red dots , using " Multiplication principle " :
The number of ways from ( 0 , 0 ) to ( 1 , 1 ) multipied by the number of ways from ( 1 , 1 ) to ( 2 , 2 ) multipied by the number of the ways from ( 2 , 2 ) to ( 3 , 3 ) , the result is ( 1 2 ) ( 1 2 ) ( 1 2 ) = 8
So we get that the answer is 2 0 − 8 = 1 2