Calculator is for the dull
9 9 9 7 2 − 3 × 9 9 9 8 2 + 3 × 9 9 9 9 2 = ?
The answer is 100000000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Moderator note:
Do you know how to generalize this expression?
Hint: 3 = ( 1 3 ) = ( 2 3 ) .
Did the same way (+1)
Log in to reply
That's nice. I was intrigued by this identity: ( n + 2 ) 2 = ( n − 1 ) 2 − 3 n 2 + 3 ( n + 1 ) 2 , hence decided to post a problem on it ;)
Log in to reply
That's really nice. Keep posting awesome problems like this.
Great, I had done by Abhay's method with slight modifications. This problem should be level 3 :thinkingface: Nice.. :+1:
⇒ 9 9 9 7 2 − 3 × 9 9 9 8 2 + 3 × 9 9 9 9 2
⇒ 9 9 9 7 2 − 3 [ 9 9 9 8 2 − 9 9 9 9 2 ]
⇒ 9 9 9 7 2 − 3 [ 1 9 9 9 9 7 × ( − 1 ) ]
⇒ 9 9 9 7 2 + 1 9 9 9 9 7 × 3
⇒ ( 1 0 0 0 0 − 3 ) 2 + [ ( 1 0 0 0 0 + 9 9 9 7 ) × 3 ]
Let 1 0 0 0 0 = a .
⇒ ( a − 3 ) 2 + ( a + 9 9 9 7 ) × 3
⇒ a 2 − 3 a + 3 0 0 0 0
⇒ 1 0 0 0 0 2 − 3 0 0 0 0 + 3 0 0 0 0 = 1 0 0 0 0 0 0 0 0
did the same way (Upvoted)
Let 9 9 9 7 = x
x 2 − 3 ( x + 1 ) 2 + 3 ( x + 2 ) 2
x 2 − 3 ( x 2 + 2 x + 1 ) + 3 ( x 2 + 4 x + 4 )
x 2 − 3 x 2 − 6 x − 3 + 3 x 2 + 1 2 x + 1 2
x 2 + 6 x + 9
( x + 3 ) 2
Substitute x
( 9 9 9 7 + 3 ) 2
1 0 0 0 0 2
1 0 0 0 0 0 0 0 0
Let a = 1 0 4 . Then we have:
( a − 3 ) 2 − 3 ( a − 2 ) 2 + 3 ( a − 1 ) 2 = a 2 − 6 a + 9 − 3 ( a 2 − 4 a + 4 ) + 3 ( a 2 − 2 a + 1 ) = a 2 = 1 0 8 = 100 000 000
x= 9999 (9997)^2 - 3 (9998)^2 + 3 (9999)^2 (x-2)^2 - 3 (x - 1)^2 + 3 (x)^2 x^2 -4x +4 - 3x^2 +6x -3 +3x^2 x^2 +2x +1 (x+1)^2 (9999 +1 )^2 (10000)^2 = 100000000
LaTeX, @Ivan Tanuwijaya ?
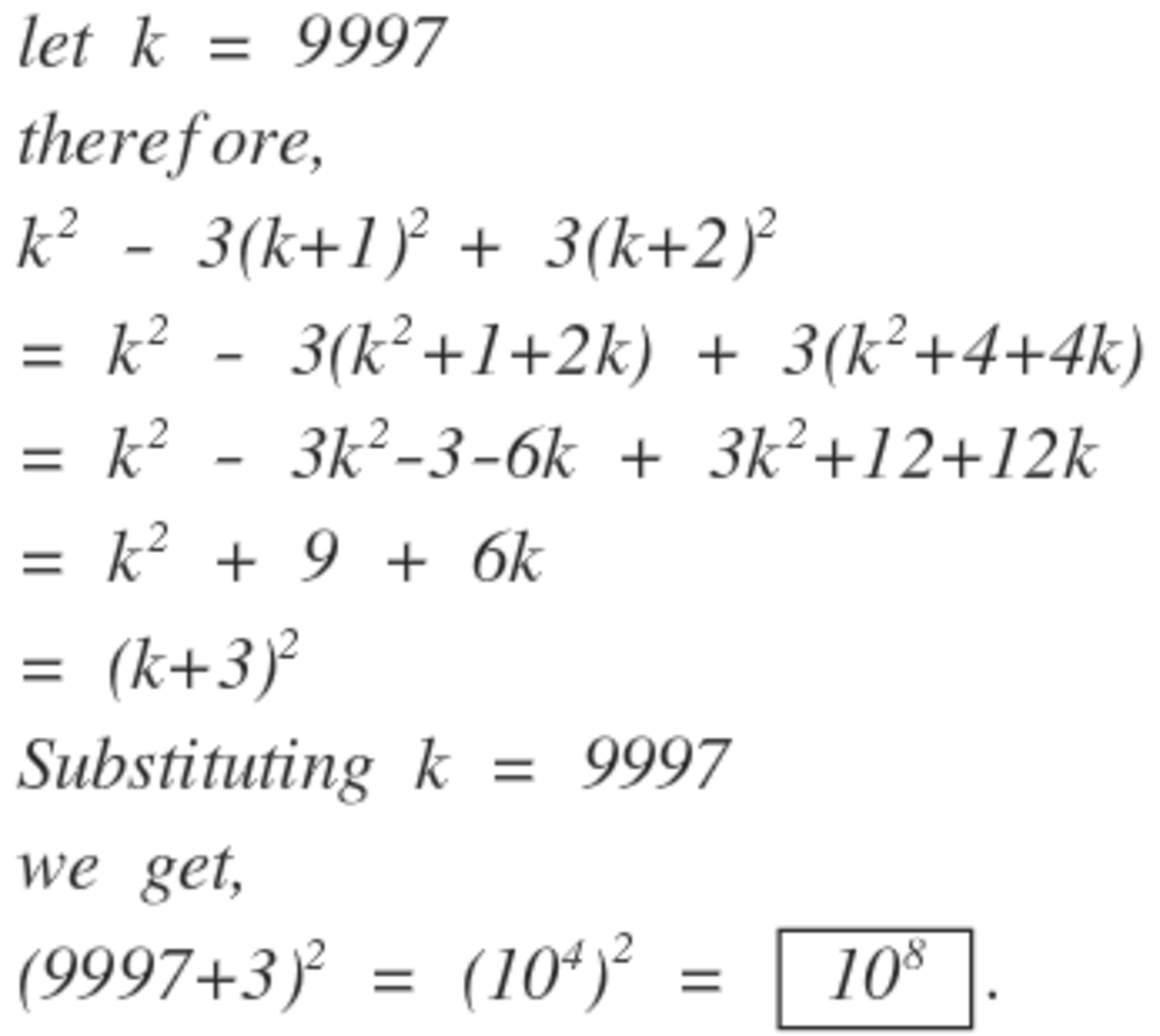
Let 9 9 9 8 = n then the expression turns to:
( n − 1 ) 2 − 3 n 2 + 3 ( n + 1 ) 2
= n 2 − 2 n + 1 − 3 n 2 + 3 n 2 + 6 n + 3
= n 2 + 4 n + 4
= ( n + 2 ) 2
Re-substituting 9 9 9 8 = n we have:
( n + 2 ) 2 = ( 9 9 9 8 + 2 ) 2 = ( 1 0 0 0 0 ) 2 = 1 0 0 0 0 0 0 0 0