Monte Carlo Method using random (x,y,z) points to find volume.

Computer Science Level 4

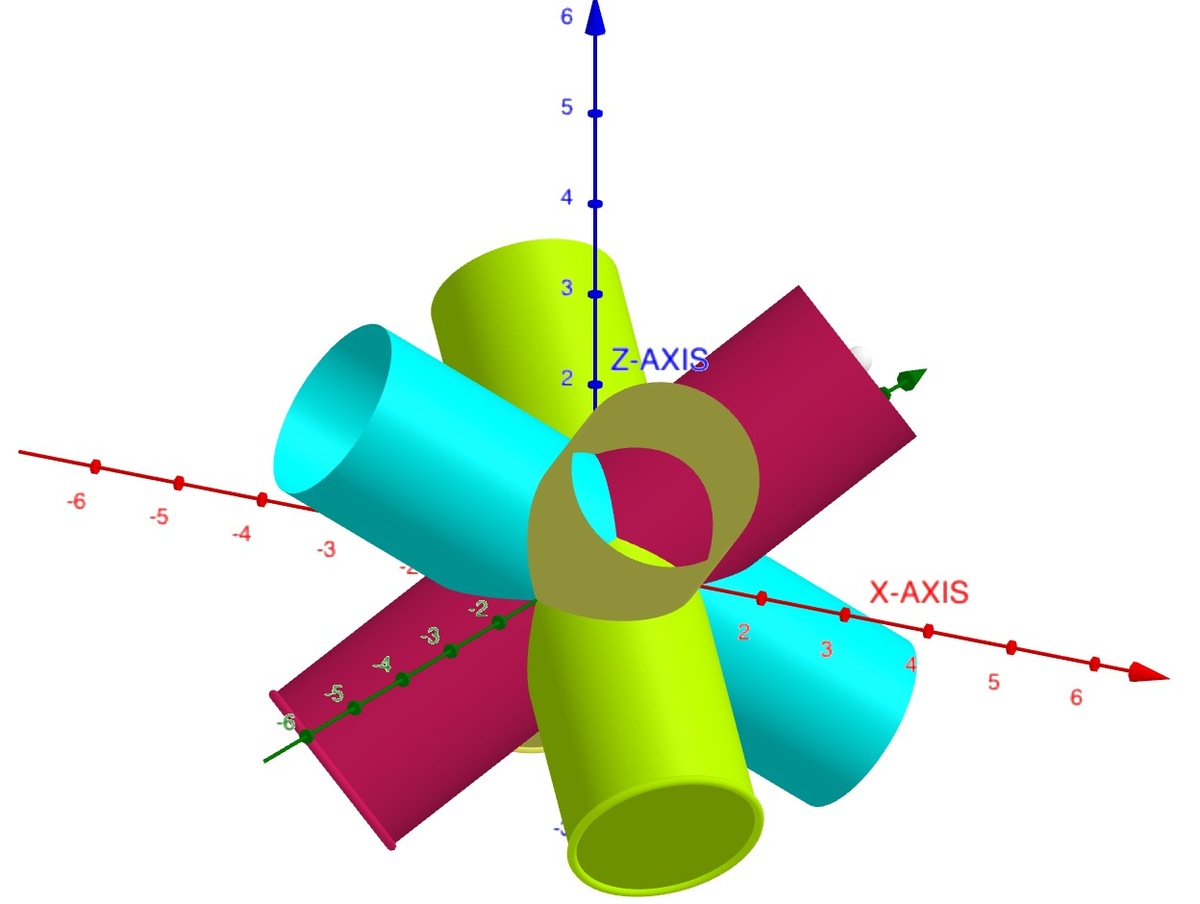
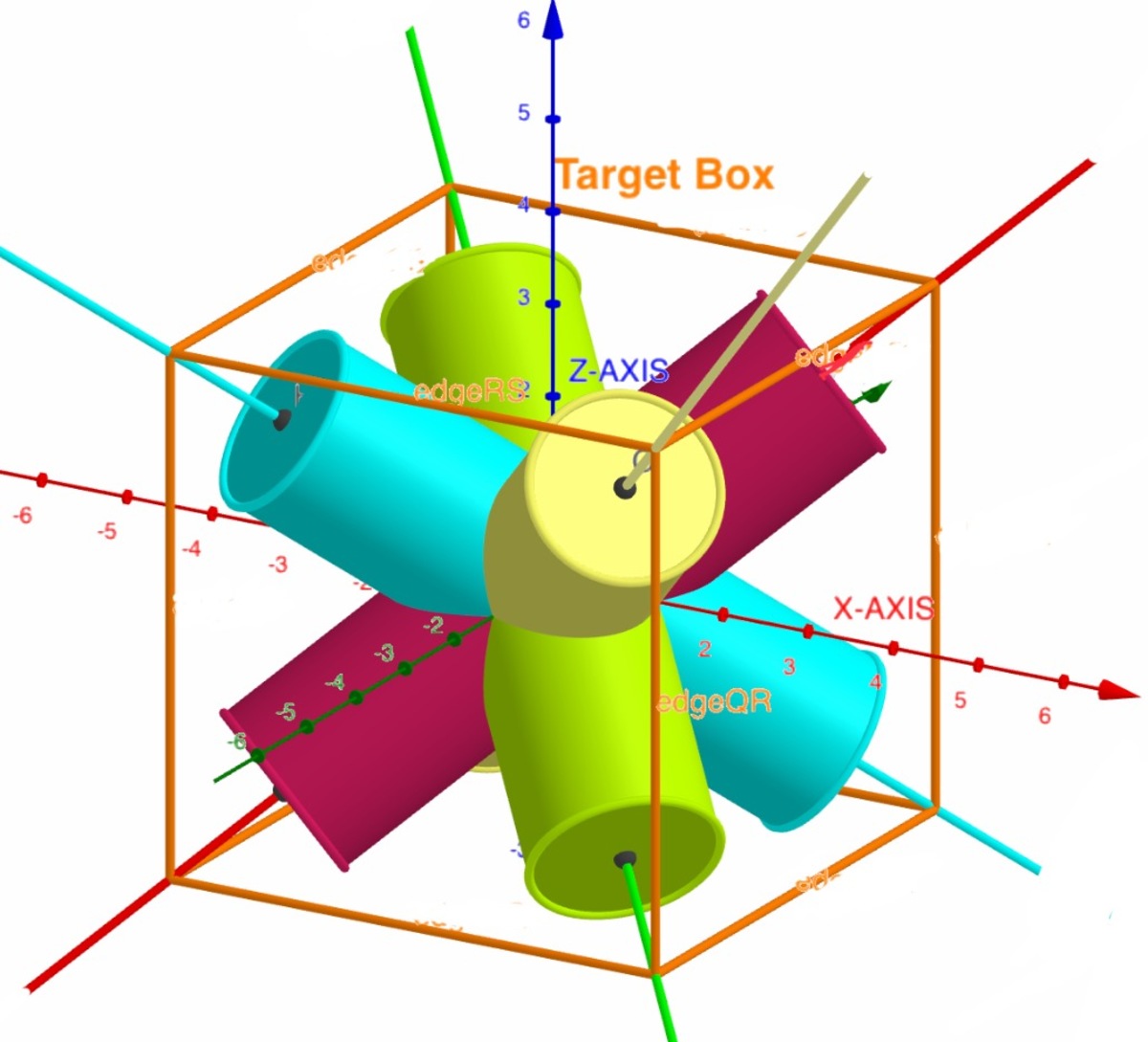
Given four RED,GREEN,BLUE,YELLOW cylinders with radius 1 each having a center line the diagonal of a cube with a volume of 64. Find their volume of intersection. Use GeoGebra or any other Graphics package to solve the problem.

The answer is 4.5.

4 solutions

Piotr Idzik
May 22, 2020

Below you will find my C++ code using multithreading. Due to the symmetry, I performed the computation on one of the octants and multiplied the result by $8$ .

#include <iostream>
#include <cmath>
#include <random>
#include <vector>
#include <chrono>
#include <thread>
#include <ctime>
#include <algorithm>

template<std::size_t Dimension, typename ValueType, typename RandomEngineType, typename IsInsideType>
class McWorker
{
    private:
        const IsInsideType isInside;
        const std::uintmax_t localIter;
        std::array<std::uniform_real_distribution<ValueType>, Dimension> pointGenerator;
        RandomEngineType randomEngine;
        ValueType amountInside;

    public:
        explicit McWorker(const std::array<std::pair<ValueType, ValueType>, Dimension>& _limitBox,
                          const IsInsideType& _isInside,
                          const std::uintmax_t _localIter,
                          const int _seed) :
        isInside(_isInside),
        localIter(_localIter),
        pointGenerator(),
        randomEngine(_seed),
        amountInside()
        {
            for(std::size_t curDim = 0; curDim < Dimension; ++curDim)
            {
                const auto curLimit = _limitBox[curDim];
                this->pointGenerator[curDim] = std::uniform_real_distribution<ValueType>(curLimit.first,
                                                                                         curLimit.second);
            }
        }
        void operator()()
        {
            for(std::uintmax_t curIter = 0; curIter < this->localIter; ++curIter)
            {
                const auto curPos = this->getRandomPoint();
                if(this->isInside(curPos))
                {
                    ++this->amountInside;
                }
            }
        }
        ValueType GetAmountInside() const
        {
            return this->amountInside;
        }
    private:
        std::array<ValueType, Dimension> getRandomPoint()
        {
            std::array<ValueType, Dimension> res;
            for(std::size_t curDim = 0; curDim < Dimension; ++curDim)
            {
                res[curDim] = this->pointGenerator[curDim](this->randomEngine);
            }
            return res;
        }
};

template<typename UnsignedIntType>
UnsignedIntType gcd(const UnsignedIntType _a, UnsignedIntType _b)
{
    UnsignedIntType a, b;
    if(_a > _b)
    {
        a = _a;
        b = _b;
    }
    else
    {
        a = _b;
        b = _a;
    }
    while(b > 0)
    {
        const UnsignedIntType div = a%b;
        a = b;
        b = div;
    }
    return a;
}

template <std::size_t Dimension, typename ValueType>
ValueType getTotalMeasure(const std::array<std::pair<ValueType, ValueType>, Dimension>& limitBox)
{
    auto prodFun = [](const ValueType tmpProd, const std::pair<ValueType, ValueType>& curDim)->ValueType
    {
        return tmpProd*(curDim.second-curDim.first);
    };
    return std::accumulate(limitBox.begin(), limitBox.end(), ValueType(1), prodFun);
}

template <std::size_t Dimension, typename ValueType, typename RandomEngineType, typename IsInsideType>
ValueType MeasureMcPar(const std::array<std::pair<ValueType, ValueType>, Dimension>& limitBox,
                       const IsInsideType& isInside,
                       const std::uintmax_t totalIter,
                       const unsigned numberOfThreads)
{
    if(totalIter%std::uintmax_t(numberOfThreads) != 0)
    {
        throw std::invalid_argument("totalIter must be a multiple of numberOfThreads.");
    }
    const std::uintmax_t localIter = totalIter/std::uintmax_t(numberOfThreads);
    std::vector<std::thread> threadVector;
    typedef McWorker<Dimension, ValueType, RandomEngineType, IsInsideType> WorkerType;
    threadVector.reserve(numberOfThreads);
    std::vector<WorkerType> workerVector;
    workerVector.reserve(numberOfThreads);
    const auto mainSeed = time(NULL);
    for(unsigned i = 0; i < numberOfThreads; ++i)
    {
        workerVector.push_back(WorkerType(limitBox, isInside, localIter, i+mainSeed));
        threadVector.push_back(std::thread(std::ref(workerVector[i])));
    }
    for(auto & th : threadVector)
    {
        th.join();
    }

    auto sumFun = [](const std::uintmax_t tmpSum, const WorkerType& inWorker)->std::uintmax_t
    {
        return tmpSum+inWorker.GetAmountInside();
    };
    const std::uintmax_t totalSum = std::accumulate(workerVector.begin(), workerVector.end(), 0ULL, sumFun);
    const auto div = gcd(totalSum, totalIter);
    const auto limitingMeasure = getTotalMeasure<Dimension, ValueType>(limitBox);
    return limitingMeasure*ValueType(totalSum/div)/ValueType(totalIter/div);
}

template <std::size_t Dimension, typename ValueType>
std::array<ValueType, Dimension> operator-(const std::array<ValueType, Dimension>& startPos,
                                           const std::array<ValueType, Dimension>& endPos)
{
    std::array<ValueType, Dimension> res;
    for(std::size_t i = 0; i < Dimension; ++i)
    {
        res[i] = endPos[i]-startPos[i];
    }
    return res;
}

template <std::size_t Dimension, typename ValueType>
ValueType normL2(const std::array<ValueType, Dimension>& inVec)
{
    auto sumSq = [](const ValueType& tmpSum, const ValueType& inVal)->ValueType
    {
        return tmpSum+inVal*inVal;
    };
    return std::sqrt(std::accumulate(inVec.begin(), inVec.end(), ValueType(0), sumSq));
}

template <typename ValueType>
std::array<ValueType, 3> crossProd(const std::array<ValueType, 3>& a,
                                   const std::array<ValueType, 3>& b)
{
    std::array<ValueType, 3> res;
    res[0] = a[1]*b[2]-a[2]*b[1];
    res[1] = a[2]*b[0]-a[0]*b[2];
    res[2] = a[0]*b[1]-a[1]*b[0];
    return res;
}

template <typename ValueType>
ValueType getDist(const std::array<ValueType, 3>& inPos,
                  const std::array<ValueType, 3>& posA,
                  const std::array<ValueType, 3>& posB)
{
    //returns the distance between the point inPos and a line determined by posA and posB
    const auto diff01 = inPos-posA;
    const auto diff02 = inPos-posB;
    const auto diff12 = posA-posB;
    const auto crossRes = crossProd(diff01, diff02);
    return normL2(crossRes)/normL2(diff12);
}

template<typename ValueType>
class IsInsideSet
{
    private:
        const ValueType r = 1;
        const std::array<ValueType, 3> posA0 = {1, 1, 1};
        const std::array<ValueType, 3> posA1 = {-1, -1, -1};
        const std::array<ValueType, 3> posB0 = {-1, 1, 1};
        const std::array<ValueType, 3> posB1 = {1, -1, -1};
        const std::array<ValueType, 3> posC0 = {1, -1, 1};
        const std::array<ValueType, 3> posC1 = {-1, 1, -1};
        const std::array<ValueType, 3> posD0 = {1, 1, -1};
        const std::array<ValueType, 3> posD1 = {-1, -1, 1};
    public:
        bool operator()(const std::array<ValueType, 3>& inPos) const
        {
            bool res = true;
            if(getDist(inPos, this->posA0, this->posA1) > this->r)
            {
                res = false;
            }
            else if(getDist(inPos, this->posB0, this->posB1) > this->r)
            {
                res = false;
            }
            else if(getDist(inPos, this->posC0, this->posC1) > this->r)
            {
                res = false;
            }
            else if(getDist(inPos, this->posD0, this->posD1) > this->r)
            {
                res = false;
            }
            return res;
        }

};

int main()
{
    typedef long double ValueType;
    typedef IsInsideSet<ValueType> IsInsideType;
    const IsInsideType isInObj = IsInsideType();
    const ValueType limitSize = 1.3L;
    const std::array<std::pair<ValueType, ValueType>, 3> limitBox = {std::make_pair(0.0L, limitSize),
                                                                     std::make_pair(0.0L, limitSize),
                                                                     std::make_pair(0.0L, limitSize)};
    const ValueType trueVolume = 12.0L*(2.0L*sqrt(2.0L)-sqrt(6.0L));
    const unsigned numberOfThreads = std::thread::hardware_concurrency();
    const std::uintmax_t totalIter = std::uintmax_t(numberOfThreads)*50000000ULL;

    const auto startTime = std::chrono::steady_clock::now();
    const auto res = 8*MeasureMcPar<3, ValueType, std::mt19937_64, IsInsideType>(limitBox,
                                                                                 isInObj,
                                                                                 totalIter,
                                                                                 numberOfThreads);
    const auto endTime = std::chrono::steady_clock::now();
    std::chrono::duration<double> runTime = endTime-startTime;
    std::cout<<"Runtime: "<<runTime.count()<<" [s]"<<std::endl;
    std::cout<<"Number of threads: "<<numberOfThreads<<std::endl;
    std::cout<<"Number of trials: "<<totalIter<<std::endl;
    std::cout<<"result: "<<res<<" trueVolume: "<<trueVolume<<" error: "<<res-trueVolume<<std::endl;
    return 0;
}

Mark Hennings
Aug 28, 2019

This is the Steinmetz solid formed by four cylinders of radius $1$ aligned in the directions of the four altitudes of a regular tetrahedron. Its volume is $\boxed{12(2\sqrt{2}-\sqrt{6})}$ .

Hosam Hajjir
Aug 23, 2019

The volume can computed by a triple integral

$\text{Volume} = \displaystyle \int_{x=-2}^{2} \int_{y=-2}^{2} \int_{z=-2}^{2} f(x, y, z) dz \hspace{4pt} dy \hspace{4pt} dx$

where,

$f(x, y, z)=\begin{cases} 1, & \text{if } (x,y,z) \text{ is inside all cylinders}.\\ 0, & \text{otherwise}. \end{cases}$

The integral evaluates to $\approx 4.552$

Here's the code for the integral and the function, written in Visual Basic.

' ====== Triple Integration using Simpson's method ========

Public Function integrate3d(ByVal a1 As Double, ByVal b1 As Double, ByVal a2 As Double, ByVal b2 As Double, ByVal a3 As Double, ByVal b3 As Double) As Double

Dim isum As Double

Dim i, j, k, l As Integer

Dim x, y, z, w As Double

isum = 0

n1 = 200

n2 = 200

n3 = 200

h1 = (b1 - a1) / n1

For i = 0 To n1

x = a1 + i * h1

If i = 0 Or i = n1 Then

ci = 1

ElseIf i Mod 2 = 1 Then

ci = 4

Else

ci = 2

End If

h2 = (b2 - a2) / n2

For j = 0 To n2

y = a2 + j * h2

If j = 0 Or j = n2 Then

cj = 1

ElseIf j Mod 2 = 1 Then

cj = 4

Else

cj = 2

End If

h3 = (b3 - a3) / n3

For k = 0 To n3

If k = 0 Or k = n3 Then

ck = 1

ElseIf k Mod 2 = 1 Then

ck = 4

Else

ck = 2

End If

z = a3 + k * h3

isum = isum + ci * cj * ck * h1 * h2 * h3 * f3d(x, y, z)

Next k

Next j

Next i

isum = isum / 27

integrate3d = isum

End Function

'=================== Function of three variables ============================

Public Function f3d(ByVal x As Double, ByVal y As Double, ByVal z As Double) As Double

Dim umat(3, 4) As Double

Dim l(3), r(3) As Double

Dim rp(3) As Double

Dim v1(3) As Double

Dim dl(3) As Double

Dim u(3) As Double

umat(1, 1) = 1

umat(2, 1) = 1

umat(3, 1) = 1

umat(1, 2) = 1

umat(2, 2) = 1

umat(3, 2) = -1

umat(1, 3) = 1

umat(2, 3) = -1

umat(3, 3) = 1

umat(1, 4) = -1

umat(2, 4) = 1

umat(3, 4) = 1

For j = 1 To 4

For i = 1 To 3

u(i) = umat(i, j)

Next i

unorm = Sqr(3)

rp(1) = x

rp(2) = y

rp(3) = z

rpnorm = norm(rp, 3)

' now we want find the distance of (x, y, z) from the line u

rproj = dot(rp, u) / unorm

rortho = rpnorm ^ 2 - rproj ^ 2

If rortho < 0 Then rortho = 0

rortho = Sqr(rortho)

If rortho > 1 Then

f3d = 0

Exit Function

End If

Next j

f3d = 1

End Function

'============== Dot product function =========================

Public Function dot(x, y)

dot = x(1) * y(1) + x(2) * y(2) + x(3) * y(3)

End Function

Frank Petiprin
Aug 22, 2019

The key to the random number problem is to find the direction numbers for the
RED,GREEN,BLUE,YELLOW cylinders center lines and use those numbers to find four planes through the origin 
perpendicular to each of four cylinders. The four sets of direction numbers become the normal vectors for each 
of the four planes.

import numpy as np
def dsqC(xpl,ypl,zpl,con): #dsqC determines circle and plane properties of point array (px,py,pz)
    global px,py,pz,radSQ
#Equation of line X=(px,py,pz)+(t*xpl,t*ypl,t*zpl) that is perpendicular to the plane and passes through (px,py,pz)
    tNumer=(con-np.multiply(xpl,px)-np.multiply(ypl,py)-np.multiply(zpl,pz))
    tDenom=(np.multiply(xpl,xpl)+np.multiply(ypl,ypl)+np.multiply(zpl,zpl))
    t=np.divide(tNumer,tDenom) #Solving for t gives a point on the plane and on the line X
    xptP,yptP,zptP=px+t*xpl,py+t*ypl,pz+t*zpl #Point (xptP,yptP,zptP) is on the plane and the line X
    dsqC=np.array(xptP**2+yptP**2+zptP**2)#Square of the Distance (xptP,yptP,zptP) is from (0,0,0)
    result=(dsqC<=radSQ) #result is a True Or False array. if True then a point was in the intersection 
    px,py,pz=px[result],py[result],pz[result] #px,py,pz contains only points in the intersection
    return   
#Begin Main
global px,py,pz,radSQ
seed=9015
#np.random.seed(seed) #Use as neded for testing
CylC=['Red','Green','Blue','Yellow']
plrgbyC=[[1,1,1,0],[-1,1,1,0],[-1,-1,1,0],[+1,-1,1,0]] #Four planes perpendicular to each cylinder at Origin.
ind,Trials,Attempts,TotVolRGBY,cntRGBY=0,10,300000000,0,0 #Index,Trials,Attempts,Overall Average,Count Of Intersects
TarS=2*2.85 #Target Side Length
TarVol=(2*TarS)**3 #Vol. of Target Cube and it Approximates the intesect Vol.(Used geogebra to find Approx. vol.)
rad=1
radSQ=rad**2
for i in range(1,Trials+1):
    px,py=np.random.uniform(-TarS,TarS,Attempts),np.random.uniform(-TarS,TarS,Attempts)
    pz=np.random.uniform(-TarS,TarS,Attempts)
#Each time through the loop will eliminate points not in the Red,Blue,Green,Yellow Cylinders.
    for j in range(0,4):
        x,y,z,con=plrgbyC[j][0],plrgbyC[j][1],plrgbyC[j][2],plrgbyC[j][3]
        dsqC(x,y,z,con)
        print(CylC[j],' Hits',len(px))
        cntRGBY=len(px)
    VolRGBY=(cntRGBY/Attempts)*TarVol
    print('Total Hits',cntRGBY,'Vol. Of The RGBY Intersect',VolRGBY,'Trial',i)
    print('------------------------------------------------------------------')
    TotVolRGBY+=VolRGBY
print('Average RGBY Intersection',TotVolRGBY/Trials,'Each Trial made ',Attempts,'Attempts')
#Run Of Ten Trials
Red  Hits 11572115 
Green  Hits 1146763 
Blue  Hits 957541 
Yellow  Hits 921970 
Total Hits 921970 Vol. Of The RGBY Intersect 4.5531304056 Trial 1
------------------------------------------------------------------
Red  Hits 11570892 
Green  Hits 1145338 
Blue  Hits 956111 
Yellow  Hits 920293 
Total Hits 920293 Vol. Of The RGBY Intersect 4.5448485746400005 Trial 2
------------------------------------------------------------------
Red  Hits 1156782
Green  Hits 1145905 
Blue  Hits 956936 
Yellow  Hits 921200 
Total Hits 921200 Vol. Of The RGBY Intersect 4.549327776 Trial 3
------------------------------------------------------------------
Red  Hits 11567033 
Green  Hits 1144607 
Blue  Hits 955986 
Yellow  Hits 920233 
Total Hits 920233 Vol. Of The RGBY Intersect 4.54455226584 Trial 4
------------------------------------------------------------------
Red  Hits 11565086 
Green  Hits 1145492 
Blue  Hits 956194 
Yellow  Hits 920478 
Total Hits 920478 Vol. Of The RGBY Intersect 4.545762193440001 Trial 5
------------------------------------------------------------------
Red  Hits 11575345 
Green  Hits 1145753 
Blue  Hits 956178 
Yellow  Hits 920697 
Total Hits 920697 Vol. Of The RGBY Intersect 4.546843720560001 Trial 6
------------------------------------------------------------------
Red  Hits 11568796 
Green  Hits 1145179 
Blue  Hits 955933 
Yellow  Hits 920364 
Total Hits 920364 Vol. Of The RGBY Intersect 4.54519920672 Trial 7
------------------------------------------------------------------
Red  Hits 11562781 
Green  Hits 1144850 
Blue  Hits 955580 
Yellow  Hits 920171 
Total Hits 920171 Vol. Of The RGBY Intersect 4.544246080080001 Trial 8
------------------------------------------------------------------
Red  Hits 11572096 
Green  Hits 1145115 
Blue  Hits 956375 
Yellow  Hits 920591 
Total Hits 920591 Vol. Of The RGBY Intersect 4.54632024168 Trial 9
------------------------------------------------------------------
Red  Hits 11570465 
Green  Hits 1144738 
Blue  Hits 956116 
Yellow  Hits 920278 
Total Hits 920278 Vol. Of The RGBY Intersect 4.54477449744 Trial 10
------------------------------------------------------------------
Average RGBY Intersection 4.546500496200001 Each Trial made  300000000 Attempts

Monte Carlo Method using random (x,y,z) points to find volume.

The answer is 4.5.

4 solutions

0 pending reports