Use sum of product of vectors T and V
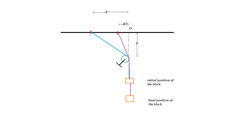 A small ring of mass
m
can slide on a friction less rod. It is connected to a block of mass
M
. The rod is at a distance
d
from the pulley. Initially the ring is at a distance
d
from point
O
. Find the velocity of the block when the ring is at a distance
d
/
2
from point
O
.
A small ring of mass
m
can slide on a friction less rod. It is connected to a block of mass
M
. The rod is at a distance
d
from the pulley. Initially the ring is at a distance
d
from point
O
. Find the velocity of the block when the ring is at a distance
d
/
2
from point
O
.
The answer is in form
V 2 = M + b m M g d ( a a − b )
Find a + b .
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Sir what about work done by tension forces?
Log in to reply
It will be negligible. This work=( elongation of the string )*Tension. The elongation is too small, and no data about the string is given.
Log in to reply
sir but the strings are ideal strings and the work done refer to mechanical work done on blocks not the elongation work done for there is no elongation in an ideal string.
Let the distance from m to point O be x, and the displacement of M from its original height be y.
By energy conservation, M g y = 2 1 m ( x ′ ) 2 + 2 1 M v 2 . By Pythagoras, distance between m and pulley is x 2 + d 2 , so y = d 2 − x 2 + d 2 .
Also, v = y ′ = d t d ( d 2 − x 2 + d 2 ) = ( x 2 + d 2 ) − 1 / 2 x x ′ , so x ′ = x v x 2 + d 2 .
Substituting x ′ and y into the energy equation, we obtain v 2 = M + ( 1 + ( x d ) 2 ) m 2 M g ( d 2 − x 2 + d 2 ) .
Since x = 2 d , we have v 2 = M + 5 m M g d ( 2 2 − 5 ) and the answer is 7 .
I used the concept that work done by tension forces in a two connected body motion is zero overall. Also using constraint relation that ,velocity of two particles in the direction of string are equal at all instants. Using these two equation i could solve for velocity of block without using calculus.
L e t t h e d i s t a n c e o f m f r o m O b e S m a n d f r o m t h e p u l l e y b e S M . B y P y t h a g o r a s S m 2 + d 2 = S M 2 . D i f f e r e n t i a t i n g S m ∗ v = S M ∗ V , w h e r e v i s t h e v e l o c i t y o f m a n d V t h e r a t e o f s h o r t e n i n g o f S M . B u t t h i s V i s a l s o t h e v e l o c i t y o f M . ∴ a t f i n a l p o s i t i o n v f = V f ∗ S M f S m f = V f ∗ ( d / 2 ) 2 + d 2 d / 2 . ∴ v f = 5 ∗ V f . . . . . . . . ( 1 )
O n l y M l o s s e s P E f a l l i n g t h r o u g h H w h i l e K E g a i n b y b o t h M a n d m . H = s h o r t e n i n g o f S M = d 2 + d 2 − ( d / 2 ) 2 + d 2 . ∴ H = d ∗ ( 2 − 2 5 ) . . . . . . . . . . . . . . . . . ( 2 ) K E g a i n = P E l o s s ⟹ 2 1 M V 2 + 2 1 m v 2 = M ∗ g ∗ H F r o m ( 1 ) a n d ( 2 ) , 2 1 M ( V f ) 2 + 2 1 m ∗ ( V f ∗ 5 ) 2 = M ∗ g ∗ d ∗ ( 2 − 2 5 ) ⟹ ( V f ) 2 = M + 5 m M ∗ g ∗ d ( 2 2 − 5 ) . . ∴ a + b = 2 + 5 = 7