Use the right theorem

Geometry Level 4

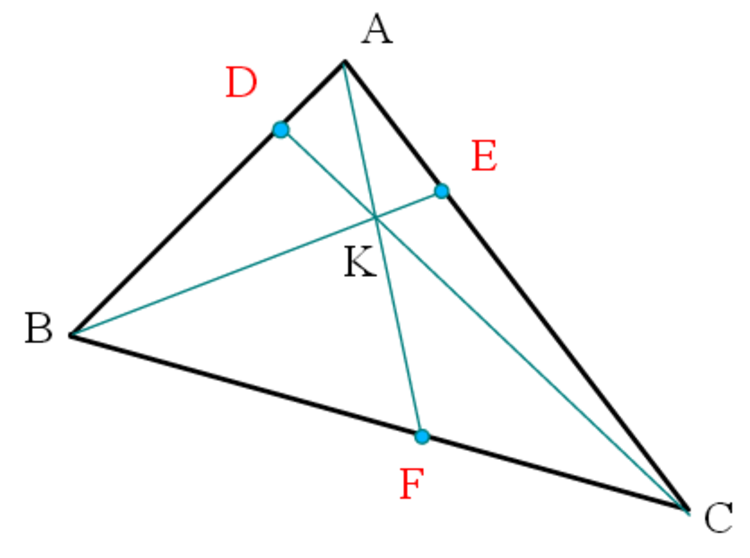In $\Delta ABC$ as shown above, straight lines are drawn from each of the vertices to their respective opposite sides and meet at point $K$ . Furthermore, $\overline{AB} = 5$ , and $\overline{AC} = 12$ .

If $\large \frac {AD}{DB} = 2\frac{AE}{EC}$ , the limiting length of $\overline {BF}$ can be expressed in the form $\frac{a}{b}$ where $a$ and $b$ are coprime positive integers. Determine $a+b$ .

The answer is 20.

1 solution

Efren Medallo
Jun 20, 2015

By Ceva's Theorem, we know that

$\frac{AD}{DB}\cdot\frac{BF}{FC}\cdot\frac{CE}{EA} = 1$

and we also know that

$\frac{AD}{DB} = 2 \frac {AE}{EC}$ ,

$2 \frac{AE}{EC}\cdot\frac{BF}{FC}\cdot\frac{CE}{EA} = 1$

$\frac{BF}{FC} =\frac{1}{2}$

To determine the limiting length of $\overline{BF}$ , we first have to note that the limiting length of $\overline{BC}$ is $17$ (by triangle inequality).

So,

$\frac{BF}{FC} =\frac{x}{17-x} =\frac{1}{2}$

solving that we get that $x = \frac {17}{3}$ , which we get $a=17$ , and $b=3$ , giving us $a+b = \boxed{20}$ .

If BC is 17 then ABC id degenerate triangle we can not determine K

Reynan Henry - 5 years, 11 months ago

I have rephrased the problem and changed the word "maximum" to "limiting". Thank you for that!

Efren Medallo - 5 years, 11 months ago

What is limiting length?

Debmalya Mitra - 5 years, 11 months ago

Did almost the same way.

Niranjan Khanderia - 4 years, 1 month ago

Use the right theorem

The answer is 20.

1 solution

0 pending reports