Use Your Eyes

Relevant wiki: Basic Composite Figures

Let the side length of the orange square be $2$ , then the radius of the blue circle is $1$ . By pythagorean theorem, the side length of the white square is $\sqrt{2}$ .

$[ORANGE~REGION]=[ORANGE~SQUARE]-[BLUE~CIRCLE]=2^2-\pi (1^2)=4-\pi \approx 0.858$

$[BLUE~REGION]=[BLUE~CIRCLE-WHITE~SQUARE]=\pi (1^2)-(\sqrt{2})^2=\pi - 2 \approx 1.142$

CONCLUSION: $\large{\boxed{\color{#3D99F6}[BLUE~REGION]\color{#333333}>\color{#EC7300}[ORANGE~REGION]}}$

NOTE:

The symbol $[]$ denotes the area.

Relevant wiki: Basic Composite Figures

Let the radius of the circle be $r$ .

The blue area is the area of the circle minus the area of the white square, or $\pi r^2 - 2r^2 = (\pi - 2)r^2 \approx 1.14r^2$ .

The orange area is the area of the large square minus the area of the circle, or $4r^2 - \pi r^2 = (4 - \pi)r^2 \approx 0.85r^2$ .

Since $1.14 > 0.85$ , the blue area is larger.

Relevant wiki: Length and Area

Without loss of generality, we may assume that the side length of the larger square is 2, i.e. the larger square has an area of 4. Notice that the white square is half as large as the larger square, i.e. it has an area of 2. Further, the radius of the circle is r=1, i.e. the circle has an area of $\pi$ . Thus the blue area is $\pi-2>3.14-2>1$ , whereas the orange area is $4-\pi<4-3.14<1$ . Hence the blue area is larger.

In general, a circle covers $\frac{\pi}{4}$ of the circumscribed square. If the circle would have covered $\frac{3}{4}$ of the square, than the blue and orange areas would have been equal, since the white square is half the area of the larger square.

$\frac{\pi}{4} > \frac{3}{4}$ , therefor the blue area is the larger of the two.

Let's call the radius of the blue circle $r$ .The white square ( $S_1$ ),the blue circle ( $S_2$ ),the orange square ( $S_3$ ).

Orange region $=S_3-S_2=(2r)^2-\pi r^2=4r^2-\pi r^2=(4-\pi)r^2 \approx 0,8584r^2$

Blue region $=S_2-S_1=\pi r^2-4\frac{r^2}{2}=\pi r^2-2r^2=(\pi-2)r^2 \approx 1.1416r^2$

Because $1.1416r^2 > 0.8584r^2$ so $\large{\boxed{\color{#3D99F6}Blue~region > \color{#EC7300}Orange~region}}$

Outer square area = 4. White square area = 2. (4 triangles, each 1/2 area of the 4 sqares that contain them. Circle area = 3.14. Orange area = 4 - 3.14 = 0.86 Blue area = 3.14 - 2 = 1.14. So A blue > A orange.

Let r = 1, then (orange area) = (2 × 2) - (1^2)pi

(Blue area) = pi - 2

(Orange area) □ (Blue area)

4 - pi □ pi - 2

6 □ 2pi

3 □ pi

3 < pi

So, Blue is larger than the Orange

Let the radius of the circle to be (r), and the lenghth of the small square to be (a)

We have the lenghth of big square = 2r And the lenghth of small square (a) = √2(r)

And thus:

Area of the big square = (2r)^2 Area of the circle = π(r)^2 Area of the small square = 2(r)^2

In the figure qe can that:

Area of Blue region A1 = π(r)^2 - 2(r)^2 = (π - 2)r^2 ~ 1.14(r)^2 Area of the Orange region A2 = (2r)^2 - π(r)^2 = (4 - π)r^2 ~ 0.85(r)^2

Now let compare A1 and A2

A1 - A2 = 1.14r^2 - 0.85r^2 ~ + 0.29r^2 > 0 So A1 > A2 --> Blue region is larger

To make it easier i would assum the side of the square as 14. So that the radius of the circle becomes 7 which easy to calculate

We can tell that the radius of the circle(r) is equal to one side of the white square(w). We can also tell that the sides of the orange square are (w + w/2). Then we find that pi(r^2) > (w + w/2)^2 for every occasion.

More easily: Let A = area of white (B) + area of blue (C); B = C + area of orange (D); for r=1 A=3.14 B=1.99 C=1.15 D=.84; Therefore D < C;

For simplicity, suppose the circle is a unit circle. So, its radius = 1, the side length of larger outer square = $2$ , and the side length of smaller square = $\sqrt{2}$

So, the area of orange region = $2^2 - \pi . 1^2 = 4 - \pi$

the area of blue region = $\pi . 1^2 - (\sqrt{2})^2 = \pi - 2$

Even if we don't use a calculator, we know that $\pi > 3$ ,

So, $\pi - 2 > 4 - \pi$

Blue > Orange

Let $l$ be the square's side length.

Note that the area of the white space is equal to $\frac{l^2}{2}$ , as it is the sum of two triangles of base $l$ and height $\frac{l}{2}$ (meaning the area of each triangle is $\frac{l^2}{4}$ ).

The are of the entire circle is $\pi \frac{l^2}{4}$ , implying the area of the blue region (circle minus white region) is $\pi \frac{l^2}{4}-\frac{l^2}{2}=\frac{\pi l^2-2l^2}{4}= \frac{l^2(\pi -2)}{4}$ .

The area of the square is $l^2$ , meaning the orange area (square minus circle) is $l^2-\pi \frac{l^2}{4}=\frac{4l^2-\pi l^2}{4}=\frac{l^2(4-\pi)}{4}$ .

Therefore, we just need to find out which is larger: $\frac{l^2(4-\pi)}{4}$ or $\frac{l^2(\pi -2)}{4}$ ? Note that $4>\pi>3$ , implying that $4-\pi<1$ and $\pi-2>1$ . Therefore, $\frac{l^2(\pi -2)}{4}$ is larger, meaning the blue area is larger.

• 
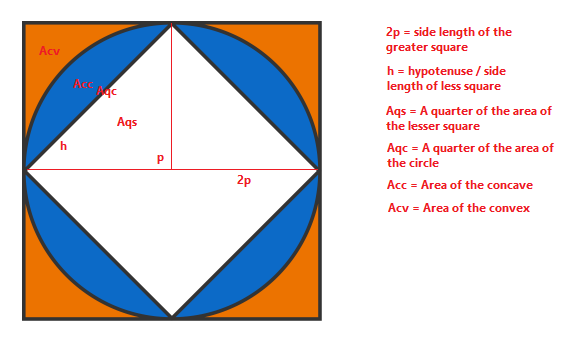
• h = p / sin (45) = sqrt(p)
• Ac = pi * p2
• Aqc = Ac/4
• Aqs = p2/2

• Acc = Aqc - Aqs

• Since the inner triangle is just half of the quarter of the greater square

• Acv = Aqs - Acc

• Acv /= Acc

• Test:

• let 2p = 8

• h = p / sin (45)

• h = 5.66

• Ac = pi * p2

• Ac = 50.27

• Aqc = Ac / 4

• Aqc = 12.57

• Aqs = p2/2

• Aqs = 16/2

• Aqs = 8

• Acc = Aqc - Aqs

• Acc = 12.57 - 8

• Acc = 4.57

• Acv = Aqs - Acc

• Acv = 8 - 4.57

• Acv = 4.43

• Acc /= Acv

• 4.57 /= 4.43 [TRUE]

Let $x$ be a side of the inscribed square and $y$ be a side of the circumscribed square and $r$ the radius of the circle.

$\implies x = \sqrt{2}r$ and $y = 2r \implies A_{orange} =(4 - \pi)r^2$ and $A_{blue} = (\pi - 2)r^2$

$A_{blue} - A_{orange} = (2\pi - 6)r^2 > 0 \implies A_{blue} > A_{orange}$ .