This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
25 solutions
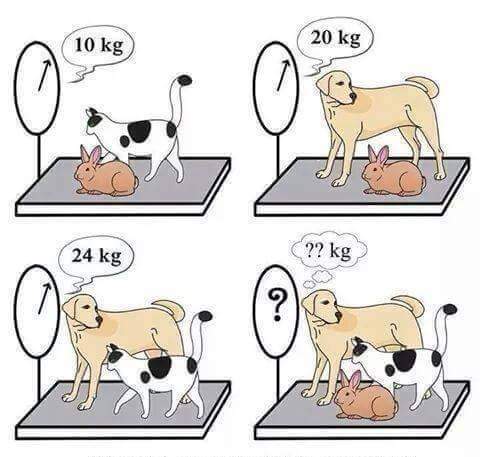
C+R=10, D+R=20, C+D=24. So... C+D+2R=30, therefore 2R=6 so R=3. C+D+3=27. Not quite to aesthetically pleasing as yours.
instead of this I have a special and simple trick we can just add all the three weights. this will become 2 animals each so we will just divide the total weight by 2 that is 54 divided by 2 will give answer 27.
O thats wonderful solution
I used matrix and elementar transformations:
1 1 0 10 1 1 0 10
0 1 1 20 ~ 1 2 1 30
1 0 1 24 1 1 1 27
Really helpful
x=(weight of cat); y=(weight of rabbit); z=(weight of dog)
From the figure,
x+y=10
z+y=20
x+z=24
Adding,
(x+y)+(z+y)+(x+z)=10+20+24
2x+2y+2z=54
2(x+y+z)=54
x+y+7=27
i.e (weight of cat)+(weight of rabbit)+(weight of dog)=27
There is a small mistype, in the end it should be x+y+z=27
x > 2 is of course: 5 < x + x^2 8! so. 28 - 1 = 28. i.e. 27 + 1 = 28.
Apparently, I took the less beaten path of finding each animal's weight... the other solution is way simpler, but still, here it is.
- b + c = 10
- b + d = 20
- c + d = 24
First thing to notice is that comparing the weigh-ins with the dog, the cat weighs 4 kg more than the bunny, so...
- c = b + 4
- plug it in to the first equation
- 2b + 4 = 10
- -4 on both sides
- 2b = 6
- /2
- b = 3
- plug it back in to the first equation
- 3 + c = 10
- -3
- c = 7
- 3 + d =20
- 7 + d = 24
- d = 17
- 3 + 7 + 17 = 27
That's my thought process too
I did the same thing. Except I got an expression for y, the dog, [20-z] where z is the cat and plugged it into the cat and dog expression, x+y=24. Substitution method, it becomes x+(20-z)=24, which simplifies to x-z=4, which lends itself to the combination method since x+z=10
Add all the three total is 54. U have counted all the animals twice so half is 27 & that is d answer.
I do the same thing. Excellent
If you plus the Dog and rabbit(20kg) + the dog and the cat (24kg) = adds to 44kg now u know that cat and rabbit weights 10kg together. Minus that 10 kg from 44kg gives u 34kg 2 dogs left. Now u want to find only one of the dog means u ÷ it by 2 = 17kg one dog
So u can work out that the: Rabbit weights 3kg Cat weights 7kg Dog 17kg
Add all of them total is 27kg
Add all of them total is 27kg
Log in to reply
If you plus the Dog and rabbit(20kg) + the dog
add the weights of the two two animals (cat+rabbit=10) (dog+rabbit=20) so that total weight of a cat, a dog n 2 rabbits become 30 ( 10+20=30) as the third picture says the weight of a cat+dog= 24 so we deduct 24 from 30 (30-24=6) thus 6 will be the weight of TWO RABBITS as these rabbits are identical they must have the same weight so when we divide 6 between 2 it is 3 of each. now for the fourth picture we know that the weight of the cat n dog is 24 n if we add 3 (the weight of rabbit ) it becomes 27. that's it.
suppose, Cat =C
Dog=D
and Mouse=M
now, C +M =10 .............(1)
and, D + M=20...................(2)
subtracting (1) from (2) we get, D-C =10................(3)
again, D+C =24..................(4)
from ,(3)+(4), we get, 2D =34, or, D =17
co, C= 24 -17 =7 and M =10-7=3
now, M+D+C =3+17+7=27kg
Cat add Bunny is 10.
Cat is 7.
Bunny is 3.
7 add 3 is 10.
bunny add dog is 20. If bunny is 3,add on 17 for the dog.
3 add 17 is 20.
Dog add cat is 24 because 17 add 7 is 24.
All them together is 27. All you need to do is add the 3 for the bunny onto the cat and dog. 24 add 3 is 27.😊
My solution is to try to find the rabbit's weight, and then add it to the cat and dog's weight. If we add the first row of animals' weight, the sum is 30, and the third one is 24kg. As you can see, the two on top has two more rabbits than the third one, which has no rabbits. 30-24=6, so the two rabbits are 6kg. now we divide 6 by two because there are two rabbits and the answer is three. We add the rabbit's weight to the cat and dogs', and we get 27.
dog + cat= 24, dog+ rabbit= 20, so cat is 4 kg heavier than rabbit. cat+rabbit= 10 kg, so cat= 7, dog= 17, rabbit=3, so the solution is 27
- Cat + Rabbit = 10KG ⇥ ①
- Dog + Rabbit = 20KG ⇥ ②
- ②-① = Cat + Rabbit -Dog - Rabbit = Cat - Dog = 10 ⇥ ③
- Cat + Dog = 24 ⇥ ④
- ③-④ = Cat + Cat + Dog - Dog = 2Cat = 14
- Cat = 7
- Dog = 24 - 7 = 17
- Rabbit = 20 - 17 = 3
Suppose the weight of the cat is x (kg), the weight of the rabbit is y (kg) and the weight of the dog is z (kg).
From the given figure, we have:
( x + y ) + ( y + z ) + ( x + z ) = 1 0 + 2 0 + 2 4
⇒ 2 x + 2 y + 2 z = 5 4
⇒ 2 ( x + y + z ) = 5 4
⇒ x + y + z = 2 5 4
⇒ x + y + z = 2 7
So the total weight of all the three animals is 2 7 k g
 Picture
Picture
Let a is a dog, b is a rabbit & c a cat
a + b = 1 0 , b + c = 2 0 , a + c = 2 4 ⟹ a + b + b + c + c + a = 1 0 + 2 0 + 2 4 = 2 ( a + b + c ) = 5 4 ⟹ a + b + c = 2 7 (kg)s
f ( x ) + d + c + r = 27. 😄😁😀😃😄☺😊😆😇😛😜😝😋 and 😒😦😧😵😎😌😳😐😑😕😴😠😡😬😶😟😔😏
We can add the weights of the first three scales . so 2 dogs + 2 cats + 2 bunnies will have have a weight of 54 . So 1 dog + 1 cat + 1 bunny will be 27
well done . thanks for the easy solution
A simple way to solve these problems is to simply add together the three total weights and then divide by 2.
An important thing to note: the kilogram is a unit of mass, not weight.
You already know that the mass of the cat and the dog is 24kg, so all you really need to figure out is the mass of the rabbit.
Let C , D , and R be the masses of the cat, the dog, and the rabbit, respectively.
According to the diagram,
C + R = 1 0
D + R = 2 0
Therefore, C + D + 2 R = 3 0
Given C + D = 2 4 from the third part of the figure,
C + D + 2 R = 3 0
⇒ 2 4 + 2 R = 3 0
⇒ 2 R = 6
⇒ R = 3
Adding R to C + D will yield 27kg, the sum of the animals' masses.
let r be the weight of rabbit, d be the weight of dog, and c be the weight of cat.
the given equations show:
c+r=10
d+r=20
d+c= 24
Note that:
d=20-r
d=24-c
Meaning,
20-r=24-c
Also note that c+r=10 which gives us c=10-r
So, by substitution,
20-r=24-c
20-r=24-(10-r)
20-r=24-10+r
20-14=2r
6=2r
r = 3
d=20-3= 1 7
c=10-3= 7
So, r+d+c=3+17+7= 27
C+r=10. C= r+4 R+4+r=10 2r+4=10 2r=6 R=3 C=3+4=7 D=17
R+C = 10 R+D =20 C+D=24
So if we : C+R+C+D = 10+24 2C+R+D = 34
We add minus both parts -R + (-D) = 20 So: 2C+R+D-R-D= 34-20 2C=14 2C/2 = 14/2 C =7 So:R+7 =10 R= 3 D=17 C+R+D= 7+3+17 = 27
x+y=10, x+z=20, y+z=24,
y=10-x, z=20-x,
10-x + 20-x = 24, -2x + 30 - 24 =0, -2x + 6=0, -2x=-6, x=3, y=7, z=17, so x + y + z = 27
Solving simultaneously by letting Rabbit = r, Dog = d and Cat = c
c + r = 10 (i)
d + r = 20 (ii)
d + c = 24 (iii)
Now from equ. (i) and (ii) solving for r gives : 10 - c = 20 - d
☞ d - c = 10 solving this with equ.(iii) simultaneously results Cat = 7 kg, Rabbit = 3 kg and Dog = 17 kg
total weight = r + d + c = 27 kg
dog+rabbit= 20 dog+cat=24 (dog+cat)-(dog+rabbit)=4 So, Cat-Rabbit= 4.. Cat+Rabbit= 10, so 7+3 then dog is 17, rabbit 3, cat 7
x+y=10 y+z=20 x+z=24 Solving x,y,z we get x=7 y=3 z=17 x+y+z= 27
Let,
Weight of Rabbit = R
Weight of Cat = C
Weight of Dog = D
Given,
C + R = 1 0 . . . . . . ( i )
D + R = 2 0 . . . . . . ( i i )
D + C = 2 4 . . . . . . ( i i i )
Adding all equations we get,
2 ( C + D + R ) = 5 4
C + D + R = 2 5 4
C + D + R = 2 7 = A n s w e r
Let the cat be represented by c, the dog by d and the rabbit by r R+C=10 - eqn 1 D+R=20 - eqn2 D+C=24 - eqn3 Add eqn 2 and 3 together 2D +R+C= 44 But R+C = 10 2D+10=44 Collect like terms 2D= 34 D=17 In eqn 2 17+R=20 R=3 but R+C=10, sub R C=10-3=7 Therefore the sum of their weight, D+C+R=17+7+3=27
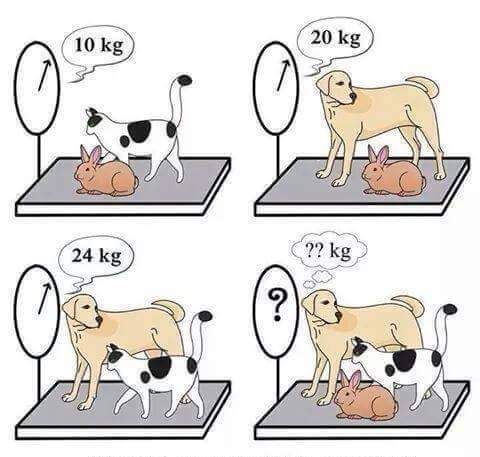
Suppose the weight of the cat be x , weight of the rabbit be y and weight of the dog be z :
Hence according to the given figure,
( x + y ) + ( y + z ) + ( x + z ) = 1 0 + 2 0 + 2 4
⇒ 2 x + 2 y + 2 z = 5 4
⇒ 2 ( x + y + z ) = 5 4
⇒ x + y + z = 2 7 .
Hence the total weight of all the three animals is 27 kg. □