Using the Sine Rule for Ambiguous Cases
Click this link if it is hard to understand the picture.
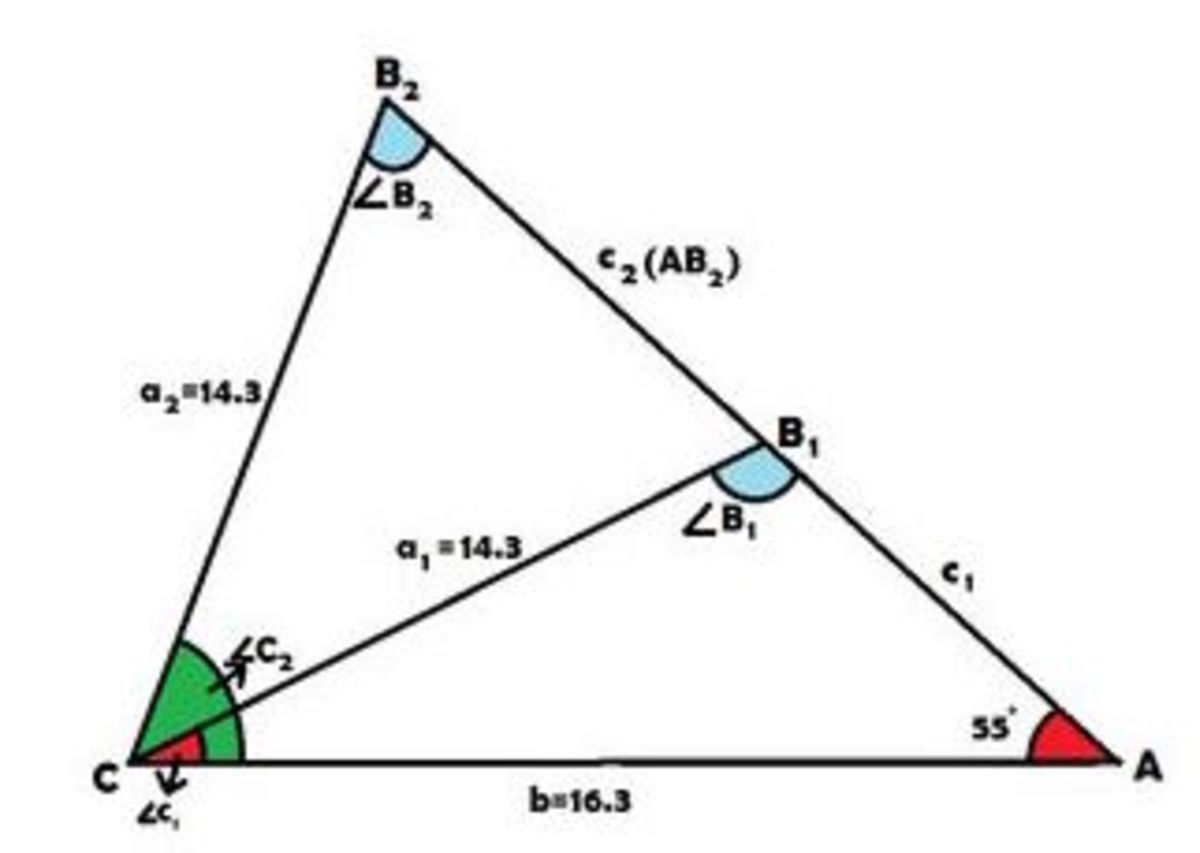
Firstly, Solve △ A B C where A ^ = 5 5 ∘ , b 1 = b 2 = 1 4 . 3 ㎝ a n d b = 1 6 . 3 c m .
Find out the sum of all the angles and add it to the sum of all the sides. (Correct to 1 decimal places.)
i.e.,
A ^ + B 1 ^ + B 2 ^ + C 1 ^ + C 2 ^ + A B 1 + A B 2 + B 1 C + B 2 C + A C o r A ^ + B 1 ^ + B 2 ^ + C 1 ^ + C 2 ^ + c 1 + c 2 + a 1 + a 2 + b
(They both have the same value.)
For clarification, A ^ = 5 5 ∘ B 1 C = a 1 = 1 4 . 3 B 2 C = a 2 = 1 4 . 3 A C = b = 1 6 . 3 A B 1 = c 1 A B 2 = A B 1 + B 1 B 2 = c 2
Details and Assumptions:
If your answer is θ ∘ + α ∘ + β ∘ + x cm + y cm, write your answer as θ + α + β + x + y .
The answer is 368.6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
STEP 1: SOLVING △ A B C :
A set of given information that would give two possible sets of solutions is said to be ambiguous .
Thus, for ambiguous cases , two solution sets will be obtained.
From the diagram, the given angle is acute and the side facing the given angle is less than the other given side. The two sets of answers are obtained using the Sine Rule which implies that:
sin A a = sin B b = sin C c
Now,
sin 5 5 ° 1 4 . 3 = sin B 1 6 . 3 ∴ sin B = 1 4 . 3 1 6 . 3 sin 5 5 ° = 0 . 9 3 3 7 B ^ = sin − 1 0 . 9 3 3 7 = 6 9 . 0 ° o r 1 1 1 . 0 °
When B ^ = 6 9 . 0 ° , C ^ = 1 8 0 ° − ( 6 9 ° + 5 5 ° ) = 5 6 °
Now,
sin 6 9 ° 1 6 . 3 = sin 5 6 ° c ∴ c = sin 6 9 ° 1 6 . 3 sin 5 6 ° ≈ 1 4 . 5 c m
When B ^ = 1 1 1 . 0 ° , C ^ = 1 8 0 ° − ( 1 1 1 ° + 5 5 ° ) = 1 4 °
Now,
sin 6 9 ° 1 6 . 3 = sin 1 4 ° c ∴ c = sin 6 9 ° 1 6 . 3 sin 1 4 ° ≈ 4 . 2 c m
Thus the two sets of solutions are:
B 1 ^ = 1 1 1 ° , C 1 ^ = 1 4 ° , c 1 = 4 . 2 2 a n d B 2 ^ = 6 9 ° , C 2 ^ = 5 6 ° , c 2 = 1 4 . 4 7
STEP 2: ADDING THE SUM OF THE ANGLES TO THE SUM OF THE SIDES OF △ A B C : Therefore,
A + B 1 + B 2 + C 1 + C 2 + a 1 + a 2 + b + c 1 + c 2 = 5 5 + 1 1 1 + 6 9 + 1 4 + 5 6 + 1 4 . 3 + 1 4 . 3 + 1 6 . 3 + 4 . 2 + 1 4 . 4 = 3 6 8 . 6