Valentines day is coming
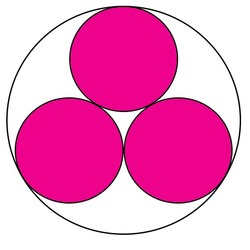All of these circles are in LOVE! See how they kiss? Well, the larger circle wants to buy the smaller pink circles dresses but doesn't know their radii. Given that the radius of the larger circle is 1, what are the radii of the smaller pink circles? (All of the circles are externally or internally tangent to their neighbors)
The answer is 0.4641.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let r = radius of pink circle. Connect the centers of two of the pink circles. The segment = 2 r. Connect those two centers to the center of the large circle. Each of those is r + x, where x is the remaining distance from the small circle to the center of the large circle. The isosceles triangle formed has a vertex angle of 120 degrees. Applying the law of cosines: (2r)^2 = ( x + r)^2 = ( x + r)^2 - 2 (x+r) (x+r) cos 120.
The radius of the large circle = 1 = x +2r. Therefore x = 1 -2r and x+r =1-2r+r = 1-r. Substitute into the previous equation, and note that cos 120 = -0.5.
4 r^2 = 2 *(1-r)^2 -2 * (1-r)^2 * -0.5 = 2 (1-r)^2 + (1-r)^2 = 3 (1-r)^2 Dividing both sides by 3: (4/3) r^2 = (1-r)^2 = 1 -2r + r^2 (1/3) r^2 = 1 - 2r Multiply by 3 and move everything to left side: r^2 - 6 r + 3 = 0 Apply Pythagoreans Theorem r = (-6 +/- sqrt(48))/2 = 0.464 ignore negative value