The Persistent Angle
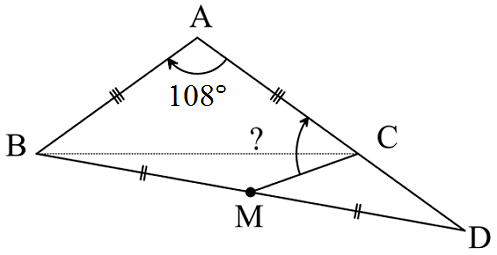
In an isosceles △ A B C , ∠ A is measured as 1 0 8 ∘ . A , C and D are collinear, while A D = B C . M is the midpoint of B D . What is the value of ∠ A C M , in degrees?
The answer is 54.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Intended solution though @Lemuel Liverosk .
i have done by the same method
It is not worthy of consideration..... Without calculator how can u compute arcsin....Any other method is acceptable
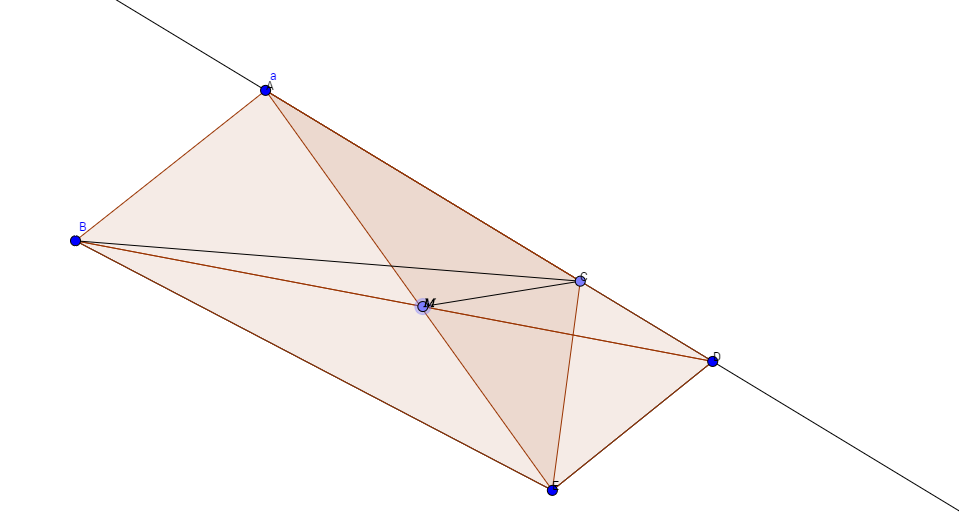
c o n s t r u c t a / / g r a m w i t h A B / / E D , A D / / B E L e t ∠ C B M b e θ ∠ A D B = ∠ D B E = 3 6 − θ B C = A D = B E . ∠ B C E = ∠ B E C = 7 2 ∠ E C D = 1 8 0 − 3 6 − 7 2 = 7 2 , ∠ C D E = ∠ A D B + B D E = 3 6 + θ + 3 6 − θ = 7 2 C E = D E = A B = A C , a n d ∠ D E C = 3 6 △ A C E i s a n i s o s . t r i a n g l e ∠ C A E = ∠ C E A = 3 6 M i s a l s o t h e m i d − p t . o f A E ∠ C M E = 9 0 a n d ∠ E C M i s 5 4 ∠ B C M = 7 2 − 5 4 = 1 8 ∠ A C M = 3 6 + 1 8 = 5 4
small typo in line-7.. Change DED to DEC.
Here's my solution. It does not require extending the diagram, but you'll probably need a calculator.
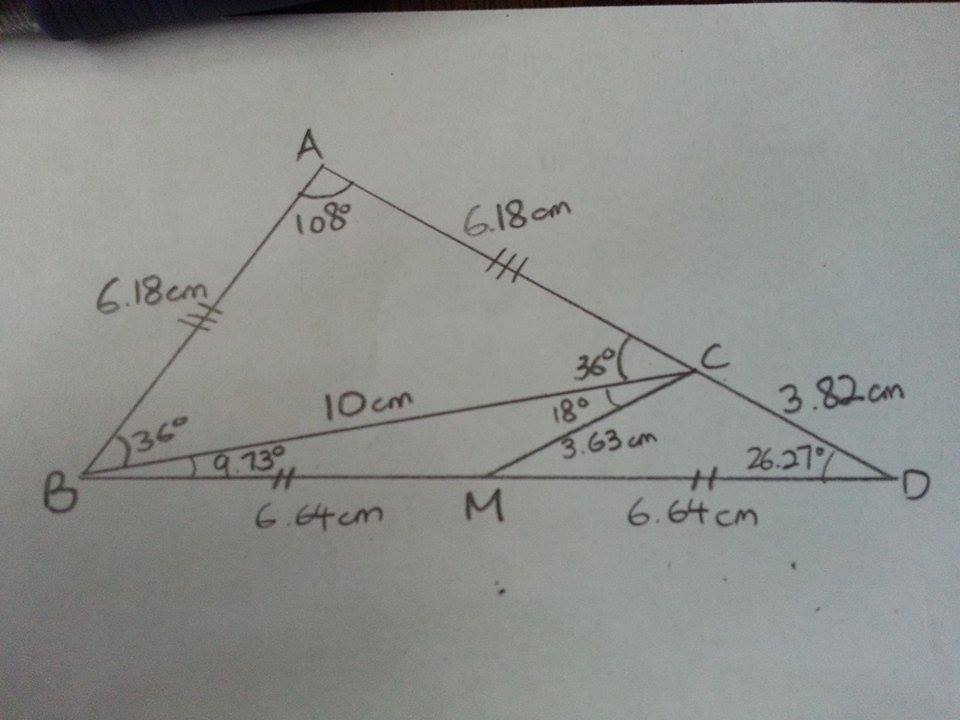
Since △ A B C is isosceles, we know that ∠ A B C = ∠ A C B = 2 1 8 0 ∘ − 1 0 8 ∘ = 3 6 ∘
Now, I let the value of B C be 1 0 cm (you can use any other value, the answer will be the same)
Next, find A C and A B with sine rule:
sin 3 6 ∘ A C = sin 1 0 8 ∘ 1 0 ⟹ A C = A B = 6 . 1 8 cm
Since A D = B C = 1 0 cm, we know that C D = 1 0 − 6 . 1 8 = 3 . 8 2 cm.
∠ B C D = 1 8 0 ∘ − 3 6 ∘ = 1 4 4 ∘
With these values, we can calculate B D with the cosine rule:
B D 2 = B C 2 + C D 2 − 2 ( B C ) ( C D ) cos ∠ B C D
B D = 1 0 2 + 3 . 8 2 2 − 2 ( 1 0 ) ( 3 . 8 2 ) cos 1 4 4 ∘ = 1 3 . 2 8 cm
Use this value obtained to find ∠ A D B :
6 . 1 8 sin ∠ A D B = 1 3 . 2 8 sin 1 0 8 ∘ ⟹ ∠ A D B = 2 6 . 2 7 ∘
We know that B M = M D = 2 1 3 . 2 8 = 6 . 6 4 cm, and ∠ C B M = 1 8 0 ∘ − 1 0 8 ∘ − 3 6 ∘ − 2 6 . 2 7 ∘ = 9 . 7 3 ∘
We need to find one more thing: the length of C M :
C M 2 = B C 2 + B M 2 − 2 ( B C ) ( B M ) cos ∠ C B M
C M = 1 0 2 + 6 . 6 4 2 − 2 ( 1 0 ) ( 6 . 6 4 ) cos 9 . 7 3 ∘ = 3 . 6 3 cm
With this, we can finally determine ∠ B C M :
6 . 6 4 sin ∠ B C M = 3 . 6 3 sin 9 . 7 3 ∘ ⟹ ∠ B C M = 1 8 ∘
Therefore, ∠ A C M = ∠ A C B + ∠ B C M = 3 6 ∘ + 1 8 ∘ = 5 4 ∘
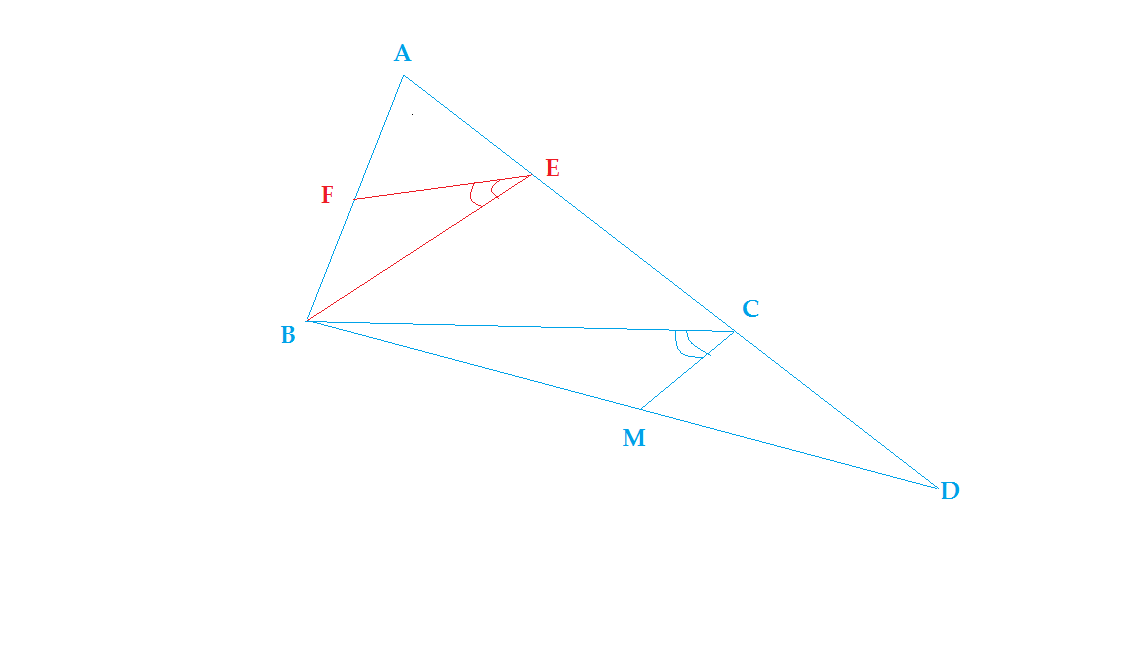
CONSTRUCTIOn:-
-
Draw a line from B || to CM and intersecting AC at E .
-
Now from E draw a line || to BC intersecting AC at F .
Let AB=AC=a and ∠ M C B = ϕ
By applying Sne Rule in △ A B C ⇒ sin ( A ) B C = sin ( B ) A C ⇒ B C = 2 . a . cos 5 π
BC =AD = 2 a cos 5 π
In △ B D E and △ M D C :-
CM || BE By BPT EC=CD = 2 . a . cos 5 π − a ⇒ A E = 2 a ( 1 − cos 5 π ) the
In △ A B C △ A F E FE || BC By BPT B C F E = A B A F = A C A E ⇒ F E = 4 . a . cos 5 π ( 1 − cos 5 π ) ) and BF=EC
Now Since FE||BC and MC||BE ∠ F E B = ∠ M C B = ϕ
By applying Sine Rule in △ B F E ⇒ sin ∠ F B E sin ∠ F E B = F E F B
This gives sin ( 5 π − ϕ ) sin ϕ = 4 . a . cos 5 π ( 1 − cos 5 π ) 2 a cos 5 π − a = 1 ⇒ sin ϕ = sin ( 5 π − ϕ )
⇒ ϕ = 1 0 π
Note:- BPT is Basic Proportionality Theorem (Thales Theorem).
So the required angle is 1 8 ∘ + 3 6 ∘ = 5 4 ∘
Draw BE // MC, where E belongs to AD. We will prove that BE is bisector of the angle ABC. Let us note m(ACB)=36= α = 5 π . Thus 0 = sin π = sin 5 α . Doing the calculus (expanding the sin 5 α ), we will get the folowing relation: 16 sin 4 α - 20 sin 2 α + 5 = 0. (1) In order to prove the BE is the bisector, we will use the theorem of bisector: "If ABC is a triangle then AM is bisector if and only if A C A B = M C M B , where M belongs to BC." Then, using the hypothesis and the auxiliary construction, we have: A B B C = A C A D = A C A C + C D = 1 + A C C E = 1 + A E + C E C E = 1 + 1 + x 1 = x + 1 x + 2 , where x = C E A E . Using the sine theorem in ABC, we will have: A B B C = s i n α s i n 3 α = 3 - 4 sin 2 α = x + 1 x + 2 . Solving the equation in x, we'll get x 1 = 4 s i n 2 α − 1 2 − 4 s i n 2 α . But, 4 s i n 2 α − 1 2 − 4 s i n 2 α = 3 - 4 sin 2 α is equivalent to 16 sin 4 α - 20 sin 2 α + 5 = 0. (1). As a conclusion, the hypothesis of bisector theorem is verified, thus A B B C = A E E C => BE bisector, so m(BEC) = 18 => m(BCM) = 18 (because BE || MC) => m(ACM) = 36 + 18 = 54.
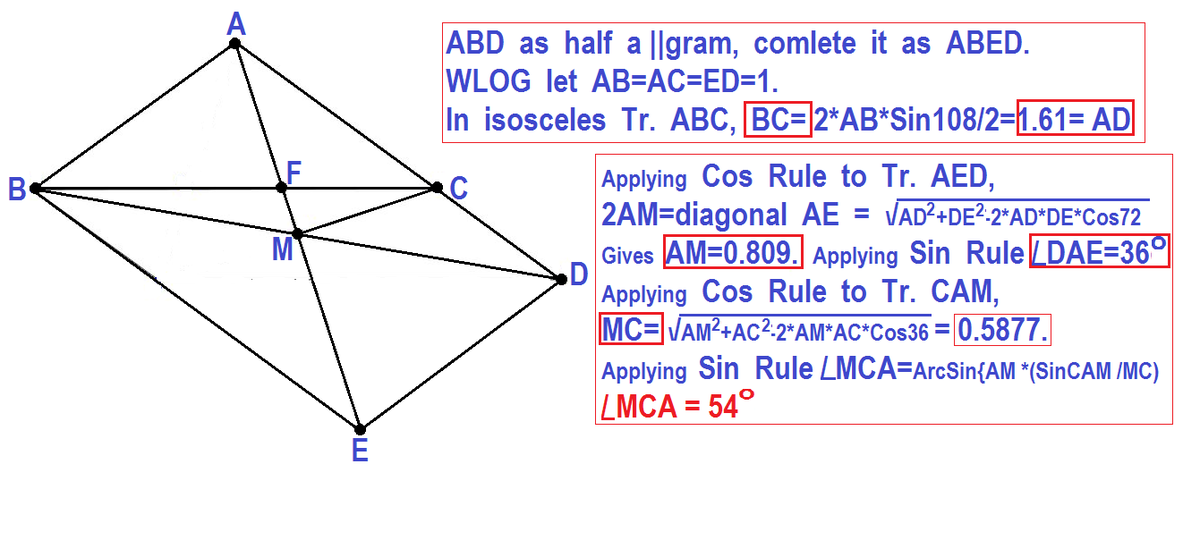
This solution may not be the best approach but is the only one I can think of right now.
A little bit background info first. An isosceles triangle with 1 0 8 ° or 3 6 ° vertex angle is rather special. The one with 1 0 8 ° has sides of ratio 1 : 1 : 2 1 + 5 , while the one with 3 6 ° as the vertex angle has sides of ratio 2 1 + 5 : 2 1 + 5 : 1 .
So here's my solution:
First, extend C M to P , making C M = M P . A P and B C intersects at Q .
B D and C P are bisecting each other, thus B C D P is a parallelogram.
Therefore, A D ∥ B P and C D = B P .
Then due to the parallel lines, B Q B P = Q C A C .
As given, B C = A D , and C D = B P , we can conclude that B P + A C = B Q + Q C .
Combining the two equations we get B P = B Q and A C = Q C .
△ A B C is isosceles and ∠ A is measured as 1 0 8 ° , which indicates that ∠ A C B and ∠ A B C are both 3 6 ° and due to parallelism, ∠ P B Q is also 3 6 ° . Therefore, △ A C Q and △ P B Q are two isosceles triangles with vertex angles measured as 3 6 ° , and △ A B C is an isosceles triangle with vertex angle measured as 1 0 8 ° .
From △ A C Q and △ P B Q we can get P Q B Q = A Q C Q = 2 1 + 5 . Then A P B C = P Q + A Q B Q + C Q = 2 1 + 5 .
From △ A B C we can get A B B C = A C B C = 2 1 + 5 .
Therefore, A B = A P = A C .
Recall that m ∠ A B C = m ∠ P B Q = 3 6 ° , we can get m ∠ A B P = 7 2 ° .
As A B = A P , △ A B P is an isosceles triangle with ∠ A B P measured as 7 2 ° . Therefore, m ∠ B A P = 3 6 ° , so m ∠ C A P = 7 2 ° . As A C = A P , △ C A P is an isosceles triangle with a 7 2 ° vertex angle, leading to the conclusion that m ∠ A C M = 5 4 ° .
And of course, an easier way is to draw the whole picture precisely and measure with a protractor.