Vanishing Electric Field
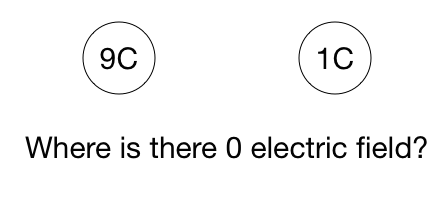
Two charges are on the x -axis. One of them is a 9 C charge located at x = 0 m . The other is a 1 C charge located at x = 1 m . Find the location on the x -axis where the net electric field due to these charges is 0 N/C .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The electric field is proportional to charge and inverse squared distance: E ∝ q / r 2 .
Thus the total electric field is zero at a points where r 1 2 q 1 = r 2 2 q 2 ∴ ( r 1 r 2 ) 2 = q 2 q 1 . Plugging in what we know, we find that the point in question is 1 / 9 = 1 / 3 closer to the second charge than to the first, giving the result 0 . 7 5 m.
How would this work for the case when the charges are 9 C and -1 C?
Log in to reply
Essentially in the same way, but now the point no longer lies between the two charges.
Once we have the 1:3 ratio, we continue:
x ± 3 1 x = L x = 1 ± 3 1 L = 3 ± 1 3 L x = 4 3 L or 2 3 L .
In the latter case, the point lies to the right of the second charge, at x = 1 . 5 0 .
E n e t = E 9 C + E 1 C = 0
E n e t = r 2 k Q 9 C r ^ 9 C + r 2 k Q 1 C r ^ 1 C = 0
Since the electric field points away from positive charges, if we choose an arbitrary point x in between the two charges, the electric field from the 9 C charge points in the positive x direction, while the electric field due to the 1 C charge points in the negative x direction at that point.
r 2 k Q 9 C x ^ + r 2 k Q 1 C ( − x ^ ) = 0
r 2 k Q 9 C x ^ = r 2 k Q 1 C ( x ^ )
x 2 Q 9 C = ( 1 − x ) 2 Q 1 C
x 2 9 = ( 1 − x ) 2 1
x = 0.75 m or 1.5 m
We must be in the region where the electric fields from the two charges point in opposite directions so that they may cancel out. Since the charges have the same sign, we must be between the two charges , so the correct answer is x = 0.75 m