Vanishing Point

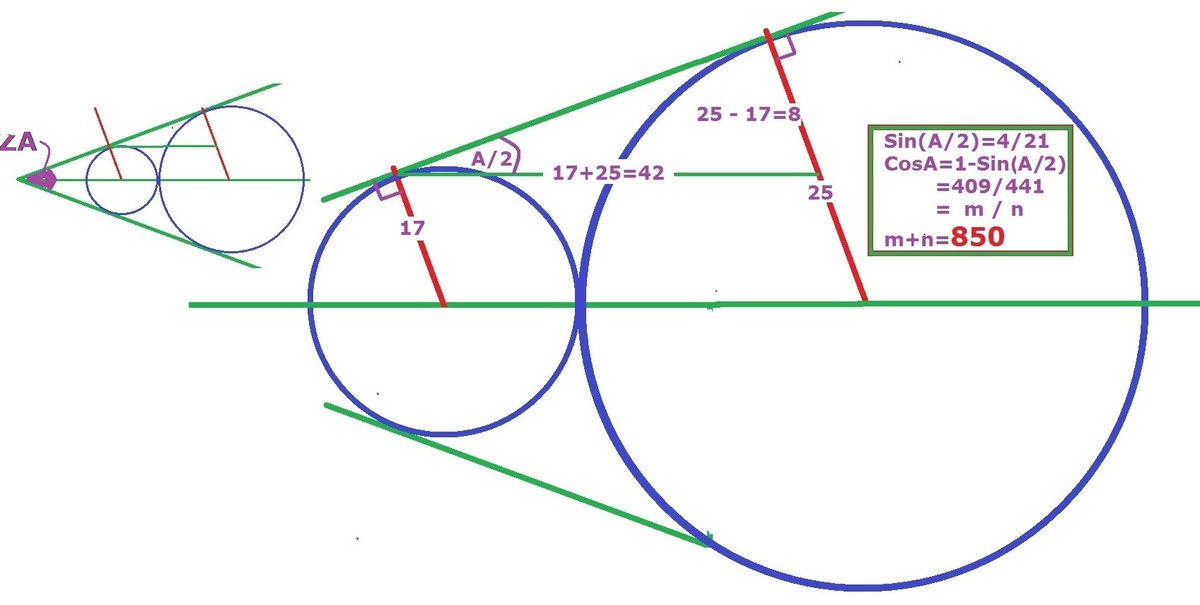
Let's let $a$ and $b$ be the radii. We get two similar right triangles if we draw one of the sides of $\angle A$ , the angle bisector of $\angle A$ (which goes through both circles' radii), and the two radii that are perpendicular to the side of $\angle A$ that we drew. The length of the part of the angle bisector (the hypotenuse) between the two radii is equal to $a + b$ .

The length of the rest of the hypotenuse, $x$ , satisfies $\frac{x}{a} = \frac{a+b}{a-b}$ by the usual similar triangle considerations. So $x = \frac{a(a+b)}{a-b}$ and so $\sin(A/2) = \frac{a-b}{a+b}$ .

Then $\cos(A) = 1-2\sin^2(A/2) = \frac{6ab-a^2-b^2}{(a+b)^2}$ . Plugging in $a = 17y$ and $b = 25y$ , we see that the $y^2$ 's on top and bottom cancel and we get $\frac{409}{441}$ , so the answer is $\fbox{850}$ .