Variable Friction on horizontal Rod !!
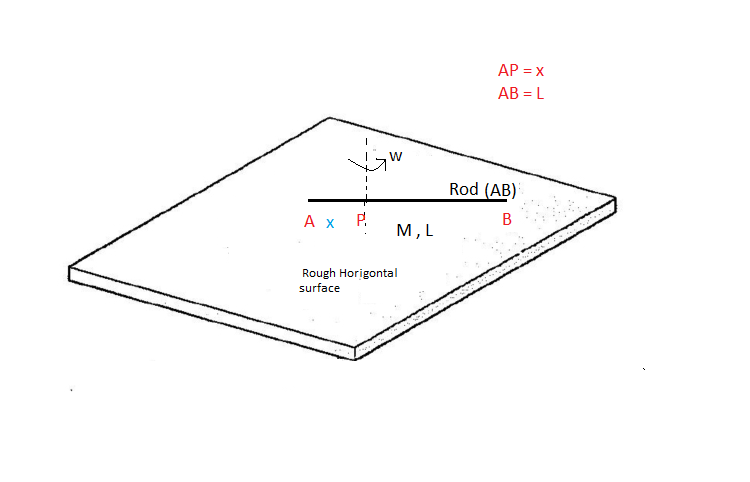 Let a uniform rod of mass
and length
is rotating with angular velocity
about an point
which is at the position of
from one end of rod .
At time zero, the rod is placed gently on a rough, level surface having coefficient of friction
.
Let a uniform rod of mass
and length
is rotating with angular velocity
about an point
which is at the position of
from one end of rod .
At time zero, the rod is placed gently on a rough, level surface having coefficient of friction
.
If the total time taken by the rod to stop completely , then for different values of position , the time taken by the rod in various experiments are different.
Suppose the maximum possible time taken for the rod to slow is and the minimum possible time is , find the value of :
.
Details
- = 10 m
- = 10 kg
- = 0.5
- = 10 m/s^2
- = 10 rad/s
#Try it's Similar Part Click here
This is Original
This is part of my set Deepanshu's Mechanics Blasts
The answer is 50.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The torque as a function of P is
τ ( P ) = L M g μ ( ∫ 0 P x d x + ∫ 0 L − P x d x ) = 2 1 M g μ ( L − 2 P + 2 L P 2 )
The rotational inertia as a function of P is
I ( P ) = L M ∫ − P L − P x 2 d x = 3 M ( L 2 + 3 P 2 − 3 L P )
The angular acceleration as a function of P is
α ( P ) = I ( P ) τ ( P ) = 2 ( L 2 + 3 P 2 − 3 L P ) 3 g μ ( L − 2 P + 2 P 2 / L )
Differentiating the acceleration with respect to P and setting it equal to zero (to find a minimum or maximum) yields P = 2 L which implies that the other (either min or max) is at an endpoint. Plugging in the values you find:
α m a x = 1 . 5 ..... which means ..... T m i n = 1 . 5 ω
α m i n = 0 . 7 5 ..... which means ..... T m a x = 0 . 7 5 ω
And thus T m a x T m i n = 0 . 5