Variable friction Work Done

Classical Mechanics Level 4

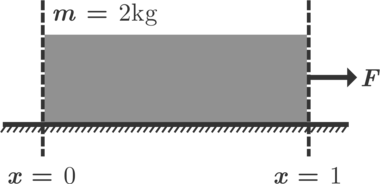
A block of mass $2 \text{ kg}$ and length $1 \text{ m}$ is placed on a rough surface (having variable kinetic friction coefficient). A horizontal force $F$ is applied such that block moves slowly. If total heat lost in this process is $\frac{4N}{3}$ Joule. Find the value of ' $N$ '.

Assume $g = 10 \text{ m/s}^2$ , ( $\mu_k = x$ for $0 \leq x \leq 1$ & $\mu_k = 0$ for $x \geq 1$ )

The answer is 5.

4 solutions

Nathanael Case
May 31, 2015

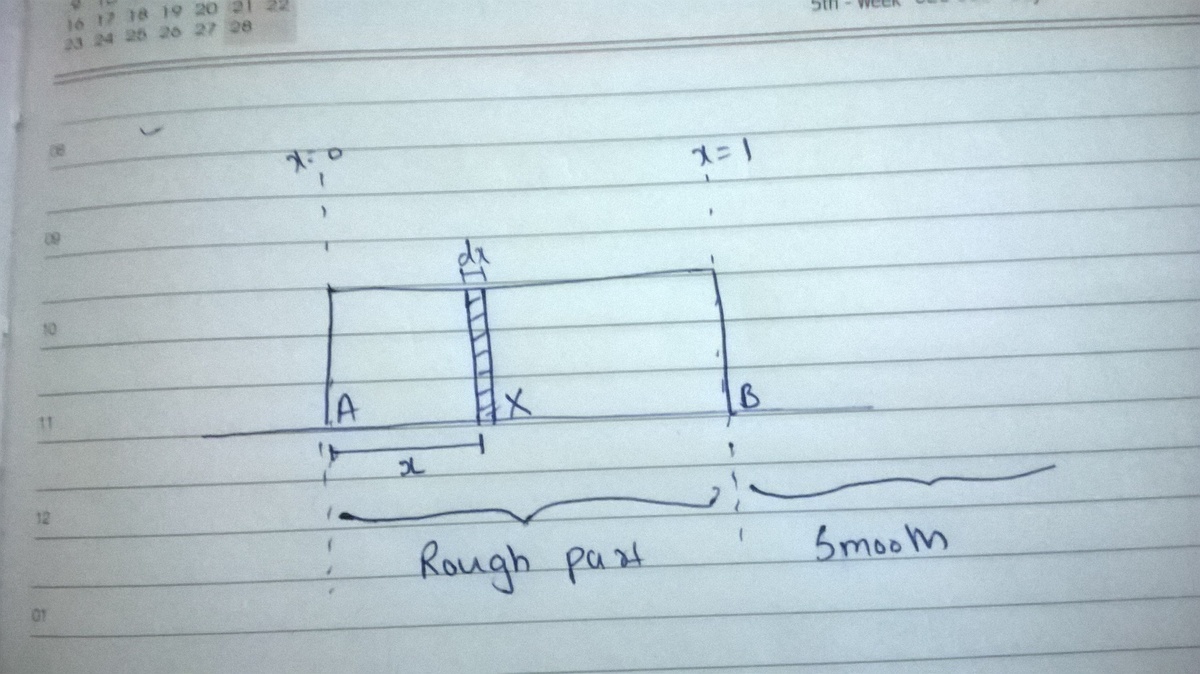
Suppose the left end of the block is at a position $x=a$ . The friction force $F_f$ will be $F_f=\int\limits_a^1 \mu dF_n$ where the differential normal force is $dF_n=gdm=mgdx$ . The problem says $\mu=x$ so the frictional force as a function of $a$ is:

$F_f=\int\limits_a^1 \mu dF_n=mg\int\limits_a^1 xdx=0.5mg(1-a^2)$

The differential work will be $F_fda$ and the total work will be equal to the amount of heat produced. Therefore we have:

$0.5mg \int\limits_0^1 (1-a^2)da=\frac{mg}{3}=\frac{4N}{3}\Rightarrow N=5$

Nicely done

Kyle Finch - 6 years ago

Rahul Badenkal
Jun 8, 2015

Usama Khidir
Jun 5, 2015

But could anybody please explain as to why the work by the force F is no taken into consideration as by the Work Energy Theorem Total Work Done = Change in Kinetic Energy

They have asked for total heat lost in the problem, which is nothing but work done by friction. It can be calculated directly as mentioned in above solutions or by subtracting change in kinetic energy from the work done by the Force F. The latter one can't be used as values of F and velocity are not given

Rahul Badenkal - 6 years ago

Avadhoot Sinkar
Jun 2, 2015

Excellent question.

Variable friction Work Done

The answer is 5.

4 solutions

0 pending reports