Variable Resistor and Bulb Energy
This is a follow-up to a problem by Charley Feng.
A circuit is set up as shown. If the variable resistor's resistance begins at at time and increases at a rate of per second, how much energy (in Joules) is dissipated in one bulb from to ?
Details and Assumptions:
- The circuit is driven by a single battery (even though it looks like two in the diagram).
- The resistance of the parallel resistor is .
- The bulbs are identical and each have a resistance of .
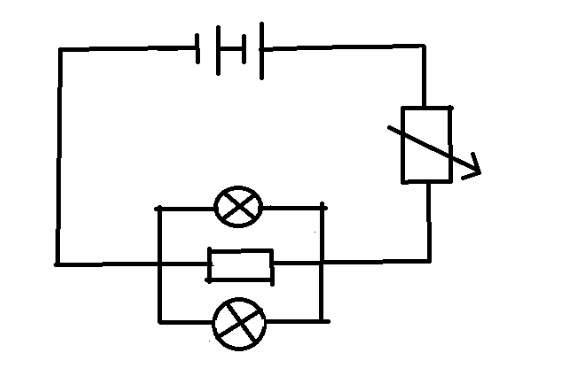
The answer is 68.57.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
E = ∫ 0 1 0 R b ( V b ( t ) ) 2 d t = ∫ 0 1 0 ( 7 + 2 t ) 2 1 2 9 6 d t = 7 + 2 t 6 4 8 ∣ ∣ ∣ ∣ 1 0 0 = 6 4 8 ( 7 1 − 2 7 1 ) ≈ 6 8 . 5 7 where R b is the resistance of the bulb.