Variation in Density!
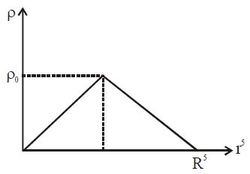 Variation of density of solid sphere of radius
with
is shown in the diagram, where
is the distance from center of the sphere. Moment of inertia of sphere about its symmetric axis is:
Variation of density of solid sphere of radius
with
is shown in the diagram, where
is the distance from center of the sphere. Moment of inertia of sphere about its symmetric axis is:
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
As the density is having spherical symmetry, let us take an element as an infinitesimally thin hollow sphere concentric with the main sphere with radius r and thickness d r .
∴ d I = 3 2 r 2 d m ( ∵ I hollow sphere = 3 2 M R 2 )
For the element, d m = ρ ⋅ d V = ρ ⋅ 4 π r 2 d r
∴ d I = 3 2 r 2 ⋅ ρ ⋅ 4 π r 2 d r
⟹ d I = 3 8 π ρ r 4 d r
⟹ I = 3 ⋅ 5 8 π ∫ 0 R ρ ⋅ 5 r 4 d r
⟹ I = 3 ⋅ 5 8 π ∫ 0 R ρ ⋅ d ( r 5 )
The above integral is simply the area under the graph of ρ vs r 5 which can be easily calculated from the above graph as 2 1 ⋅ ρ ⋅ R 5
∴ I = 1 5 4 π ρ 0 R 5