Varignon Variation
Find the minimum possible perimeter of a convex quadrilateral with four distinct integer sides that has the property that a square is formed when the midpoints of its consecutive sides are joined.
The answer is 24.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Great solution! Can you find a method to find the collection of integers (A, B, C, D) without using a computer search?
Log in to reply
A 2 + D 2 = B 2 + C 2 is the same as ∣ A + i B ∣ 2 = ∣ C + i D ∣ 2 , so we can spend time looking at factorizations in the Gaussian integers...
For example 6 5 = 5 × 1 3 = ( 2 + i ) ( 2 − i ) ( 3 + 2 i ) ( 3 − 2 i ) = 4 2 + 7 2 = 8 2 + 1 2 because ( 2 + i ) ( 3 + 2 i ) = 4 + 7 i and ( 2 + i ) ( 3 − 2 i ) = 8 − i , while 8 5 = 5 × 1 7 = ( 2 + i ) ( 2 − i ) ( 4 + i ) ( 4 − 1 ) = 7 2 + 6 2 = 9 2 + 2 2 because ( 2 + i ) ( 4 + i ) = 7 + 6 i and ( 2 + i ) ( 4 − i ) = 9 + 2 i .
Log in to reply
I did it by rearranging A 2 + D 2 = B 2 + C 2 to ( A − C ) ( A + C ) = ( B − D ) ( B + D ) and examining numbers that can be factored in two different ways, but it was a long proof.
I'm sure I've made a silly error, but I cannot seem to draw the solution quadrilateral. There are three distinct quadrilaterals when all four sides are given. Right? The lower right quadrilateral is the closest, its sides' midpoints are a rectangle, but clearly not a square. Where did I go wrong? Thanks!
Hmm. I seem unable to upload an image in a comment. Here's a link
Well, that's embarrassing. I had convinced myself that four lengths in an ordered tuple uniquely determined a quadrilateral. Like I said. Silly. Thank you.
Log in to reply
The quadrilateral has diagonals of length d that meet at right angles. One is split into lengths x , d − x , and the other into lengths. y , d − y by the intersection.
You can get pictures in comments, but it is a two-stage process. Find a solution of your own. Edit it, and add the graphic you want. Copy the generated text, and cancel out of your solution. Go back to the comment, and paste the code in...
I got to the point where I concluded that the sides should satisfy a 2 + c 2 = b 2 + d 2 . Then I just looked for appropriate numbers. Got 1 + 8 + 4 + 7 = 2 0 wrong and just went with the next possible. Your solution is once again amazing, congrats!
Use the following diagram, and let a = A B , b = B C , c = C D , d = A D , p = A C , q = B D , m = I D , n = I C , and s = E F = F G = H G = H E :
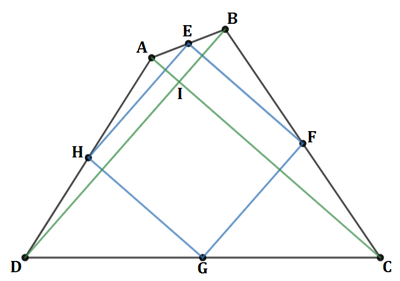
Since H E is the mid-segment of △ A B D , H E ∣ ∣ B D and q = B D = 2 H E = 2 s .
Similarly, since A C is the mid-segment of △ A B C , E F ∣ ∣ A C and p = A C = 2 E F = 2 s .
Therefore, p = 2 s = q , and since H E ⊥ E F , B D ⊥ A C . In other words, the diagonals of A B C D are both congruent and perpendicular to each other.
By the Pythagorean Theorem on △ A I B , △ B I C , △ C I D , and △ A I D , a 2 = ( p − m ) 2 + ( p − n ) 2 , b 2 = ( p − m ) 2 + n 2 , c 2 = m 2 + n 2 , and d 2 = ( p − n ) 2 + m 2 , which means that d 2 − a 2 = m 2 − ( p − m ) 2 = c 2 − b 2 , and ( d − a ) ( d + a ) = ( c − b ) ( c + b ) .
Let k = ( d − a ) ( d + a ) = ( c − b ) ( c + b ) . Without loss of generality, let d > a and d + a > c + b . Since a and d are positive distinct integers and k = ( d − a ) ( d + a ) , k must also be a positive integer. Also, since b and c are positive distinct integers and k = ( c − b ) ( c + b ) , c > b .
Also from k = ( d − a ) ( d + a ) = ( c − b ) ( c + b ) , we can also conclude that k can be factored in two different ways, and since a , b , c , and d are all distinct integers, the pairs of factors must have the same parity.
The largest that a + d = A B + A D could be would be if B C and C D were collinear and if C were at B (or D ), so that p = B D = B C + C D = b + c , and the other diagonal A C ⊥ B D would be the height of △ A B D at B (or D ), making an isosceles right triangle such that A B = a = b + c is the leg and B D = d = 2 ( b + c ) is the hypotenuse so that a + d = ( 1 + 2 ) ( b + c ) .
However, since p < b + c by the properties of a triangle, a + d < ( 1 + 2 ) ( b + c ) .
By a similar argument, c + d < ( 1 + 2 ) ( a + b ) , b + c < ( 1 + 2 ) ( a + d ) , and a + b < ( 1 + 2 ) ( c + d ) .
Let u = d − a and let v = c − b . Then by substitution k = u ( a + d ) = v ( b + c ) , which means a + d = u v ( b + c ) , and substituting this into b + c < a + d < ( 1 + 2 ) ( b + c ) gives b + c < u v ( b + c ) < ( 1 + 2 ) ( b + c ) , so that 1 < u v < 1 + 2 .
Assume d − a = u = 1 . Then since the pairs of factors of k have the same parity, a + d is also odd, which means k is odd, which means c − b = v and c + b must also be odd. However, there are no odd integers for 1 < 1 v < 1 + 2 , so d − a = u = 1 .
Let d − a = u = 2 . Then since the pairs of factors of k have the same parity, a + d is also even, which means k is even, which means c − b = v and c + b must also be even. From 1 < u v < 1 + 2 we can conclude that v = 4 . Therefore, if u = 2 then k is a multiple of 8 .
However, k = 8 because 8 does not have two different pairs of even factors. If k = 1 6 and d − a = u = 2 , then a + d = 8 , and c − b = v = 4 and c + b = 4 , which would lead to b = 0 . If k = 2 4 and d − a = u = 2 , then a + d = 1 2 , which would lead to a = 5 and d = 7 , and c − b = v = 4 and c + b = 6 , which would lead to b = 1 and c = 5 , so that a = c = 5 , which are not distinct.
But if k = 3 2 and d − a = u = 2 , then a + d = 1 6 , which would lead to a = 7 and d = 9 , and c − b = v = 4 and c + b = 8 , which would lead to b = 2 and c = 6 , all distinct integers. Therefore, a quadrilateral with distinct integer sides a = 7 , b = 2 , c = 6 , and d = 9 will have the property that a square is formed when the midpoints of its consecutive sides are joined, and its perimeter is a + b + c + d = 2 4 .
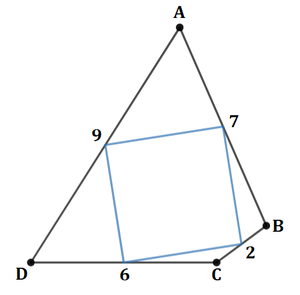
But is this the smallest perimeter possible?
Choosing larger integers for k for u = 2 leads to larger perimeters, so there are no smaller perimeters possible for u = 2 .
If u = 3 , then the smallest value for k where v is an odd integer greater than u = 3 is k = 4 5 , which leads to a = 6 , b = 2 , c = 7 , d = 9 , and P = 2 4 (the same minimum perimeter as before), and choosing larger integers for k with u = 3 leads to larger perimeters.
In general, if d − a = u , then d + a = u k , which makes d = 2 u k + u 2 and a = 2 u k − u 2 , and if c − b = v , then c + b = v k , which makes c = 2 v k + v 2 and b = 2 v k − v 2 . The perimeter is then P = a + b + c + d = u k + v k = u v k ( u + v ) . Since u and v must have the same parity, the smallest perimeter for a given k and u will be when v = u + 2 .
Substituting these values for a , b , c , and d into c + d < ( 1 + 2 ) ( a + b ) and rearranging, we find that k > ( 1 + 2 ) u v ≥ 3 u v , and substituting this and v = u + 2 into P = u v k ( u + v ) gives P ≥ 6 ( u + 1 ) . Therefore, for u ≥ 4 , P ≥ 3 0 .
Therefore, the smallest possible perimeter for a quadrilateral with the given conditions is 2 4 .
It is straightforward to show that the equilateral P Q R S can be moved so that its vertices P , R are on the x-axis and Q , S are on the y-axis. To show this, work from the inside out, we start with a square with side k ∈ R , say the square A B C D with A = ( 2 k , 2 k ) , B = ( − 2 k , 2 k ) , C = ( − 2 k , − 2 k ) , D = ( 2 k , − 2 k ) , Construct a quadrilateral P Q R S around it, starting at a point P = ( x p , y p ) and find the other vertices by point-mirroring: Q = 2 A − P , R = 2 B − Q , etc. until we are back at P. We find P = ( x p , y p ) , Q = ( k − x p , k − y p ) , R = ( − 2 k + x p , y p ) , S = ( k − x p , − k − y p ) ). Notice that P , Q , R , S are each on a side of a circum scribing square with side 2 k . Also, notice that y p = y r and x q = x s .
After the correct translation, we have
P
=
(
p
,
0
)
,
Q
=
(
0
,
q
)
,
R
=
(
−
r
,
0
)
,
S
=
(
0
,
−
s
)
and we will set
P
Q
=
a
,
Q
R
=
b
,
R
S
=
c
,
S
P
=
d
.
The convexness criterion then corresponds to
p
,
q
,
r
,
s
>
0
.
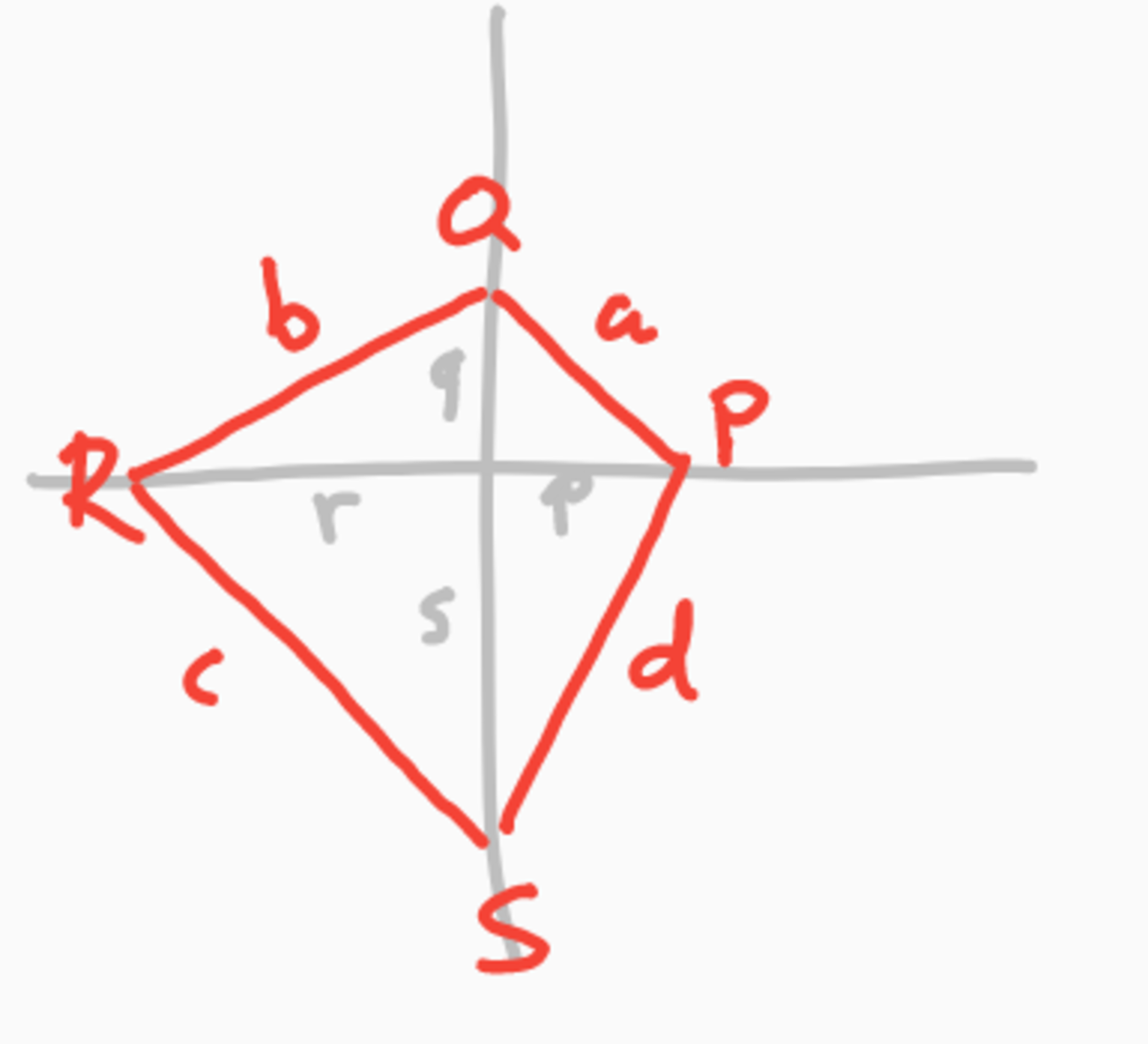
Without loss of generality we may assume that p < r ⇒ a < b ; d < c and also q < s ⇒ a < d ; b < c . By reflection in the line x = y , b and d interchange, so we can also assume that b < d and so a < b < d < c
We can identify 4 right-angled triangles and we have that the axes PR and QS have equal lengths:
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ p 2 + q 2 = a 2 q 2 + r 2 = b 2 r 2 + s 2 = c 2 s 2 + p 2 = d 2 r + p = q + s ⇒ ⎩ ⎪ ⎨ ⎪ ⎧ r 2 − p 2 = b 2 − a 2 = c 2 − d 2 s 2 − q 2 = c 2 − b 2 = d 2 − a 2 r + p = q + s
The following code searches for fit combinations of a,b,c,d, that fulfill these requirements. It outputs
a=2, b=6, c=9, d=7, perimeter=24
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
|
Log in to reply
Used the following, all enclosed in a formula:
\begin{equation} \begin{cases} p^2+q^2=a^2\ q^2+r^2=b^2\ r^2+s^2=c^2\ s^2+p^2=d^2\ r+p=q+s \end{cases}\, \end{equation} \Rightarrow \begin{equation} \begin{cases} r^2-p^2=b^2-a^2=c^2-d^2\ s^2-q^2=c^2-b^2 =d^2-a^2\ r+p=q+s \end{cases}\, \end{equation}
Varignon's Theorem tells us that, for any quadrilateral, the midpoint quadrilateral is a parallelogram. Since a side of this parallelogram will be half the length of one of the diagonals of the original quadrilateral, this parallelogram will be a rhombus provided that the original quadrilateral has diagonals of equal length. Moreover, the parallel pairs of sides of the parallelogram will be orthogonal exactly when the diagonals of the original quadrilateral are orthogonal. Thus the parallelogram will be a square precisely when the original quadrilateral has orthogonal diagonals of equal length.
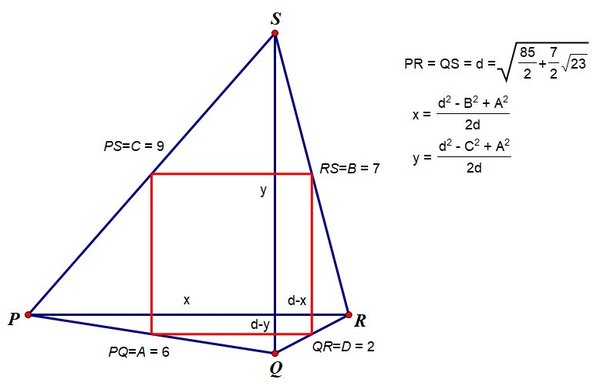
If the diagonals are of length d , we need to find 0 < x , y < d such that x 2 + y 2 = A 2 ( d − x ) 2 + y 2 = B 2 x 2 + ( d − y ) 2 = C 2 ( d − x ) 2 + ( d − y ) 2 = D 2 where A , B , C , D are distinct integers (the sides of the quadrilateral). These equations imply that
d ( d − 2 x ) = B 2 − A 2 = D 2 − C 2 d ( d − 2 y ) = C 2 − A 2 = D 2 − B 2 and hence we must have A 2 + D 2 = B 2 + C 2 and then x = 2 d d 2 − B 2 + A 2 y = 2 d d 2 − C 2 + A 2 and this will all work provided that this pair of values for x , y have their squares adding to A 2 , which implies that d must satisfy the quartic F ( d ) = 2 d 4 − 2 ( B 2 + C 2 ) d 2 + ( A 2 − B 2 ) 2 + ( A 2 − C 2 ) 2 = 0 If we assume that A > B , then A 2 + D 2 = B 2 + C 2 will require A > B > C > D . If we search for integer solutions for the equation A 2 + D 2 = B 2 + C 2 over collections of positive integers A , B , C , D such that A > B > C > D and A + B + C + D ≤ 2 4 (there are only 2 4 1 such collections of integers, so a computer search for the ones with the "sum of squares" property is in order), there are only two solutions: ( A , B , C , D ) = ( 8 , 7 , 4 , 1 ) and ( A , B , C , D ) = ( 9 , 7 , 6 , 2 ) . The first set of integers yields a quartic polynomial F ( d ) with no real roots, and so does not count. The only possible solution left is ( A , B , C , D ) = ( 9 , 7 , 6 , 2 ) , which gives a real value of d = 2 8 5 + 2 7 2 3 and OK values of x , y . Thus the minimum possible perimeter is 9 + 7 + 6 + 2 = 2 4 .