Vector

Classical Mechanics Level 1

Find the magnitude of the resultant of a force 6N due east and a force 8N due north.

2 N 23 N 5 N 10 N

Ajay Rajpurohit by Ajay Rajpurohit , 23, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

8 solutions

Mardokay Mosazghi
Jul 28, 2014

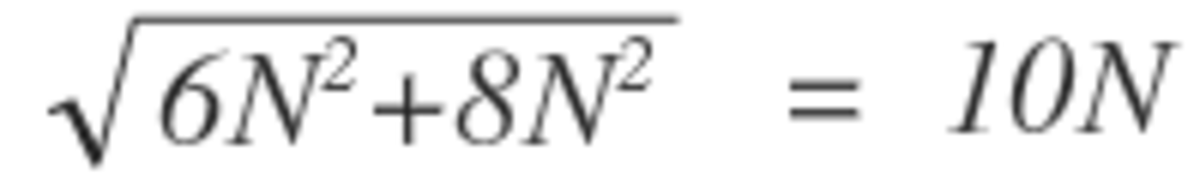
The resultant of two vectors in this case two forces is given by A 2 + b 2 \sqrt {A^2+b^2} = C C so form this we find the resultant/ magnitude by the formula resultant= ( 6 ) 2 + ( 8 ) 2 ) = 10 \sqrt {(6)^2+(8)^2)}=10

20 Helpful 0 Interesting 0 Brilliant 0 Confused

Or by using Parallelogram law of vectors.

Oshin Bhoi - 6 years, 10 months ago

Log in to reply

yeah of course

Mardokay Mosazghi - 6 years, 10 months ago
Sayan Karmakar
Jul 29, 2014

Here we can see that the resultant forces is the hypotenuse of the triangle so. {(8^2+6^2)}^1/2 N = 10 N

3 Helpful 0 Interesting 0 Brilliant 0 Confused
Fedor Panafidin
Oct 26, 2015

New vector has coordinates of (6, 8), using the Pythagorean theorem we can figure out its length : √6²+8² = √100 = 10. So the length of this vector is 10N.

1 Helpful 0 Interesting 0 Brilliant 0 Confused

I like your explanation.

Susan Naylor - 5 years, 6 months ago
Glënn Täbiölö
Sep 24, 2014

Fv=8sin90 =8 Fx=6cos0 = 6 R=√(8^2+6^2) = 10

1 Helpful 0 Interesting 0 Brilliant 0 Confused

parallelogram...but in the diagram..you must let the north line taller :p

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Achille 'Gilles'
Nov 30, 2015

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Tushar Kaushik
Sep 24, 2015

Resultant is unde root of a^2+b^2 36+64=10

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Getnet Reta
Nov 16, 2014

Write a solution. it is performed using pythagores ; In a right angled triangle: the square of the hypotenuse is equal to the sum of the squares of the other two sides. the sum of the square of the horizontal(8N) and the vertical (6N) vectores= square root of 112 which is 10N

0 Helpful 0 Interesting 0 Brilliant 0 Confused

friend you made a mistake in the solution i.e. The sum of the square of 8N and 6N is not 112 but only 100. Correct it!

Ajay Rajpurohit - 6 years, 6 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...