Vector Addition?
Classical Mechanics
Level
3
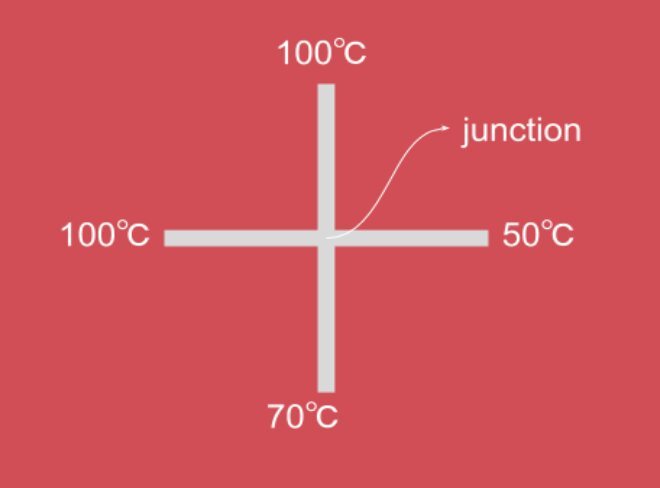 Find the temperature of junction if rods are identical and are placed symmetrically.
Find the temperature of junction if rods are identical and are placed symmetrically.
None of these
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
It follows from the solution of the time-invariant two-dimensional heat equation ∇ 2 u ( x , y ) = 0 that, temperature at any point in the steady-state is the average of the temperatures of the neighbouring points. Thus the temperature at the junction is T = 4 1 ( 1 0 0 + 1 0 0 + 5 0 + 7 0 ) ∘ C = 8 0 ∘ C