Vector problem

It is noticeable that the vectors create a parallelogram as shown in the diagram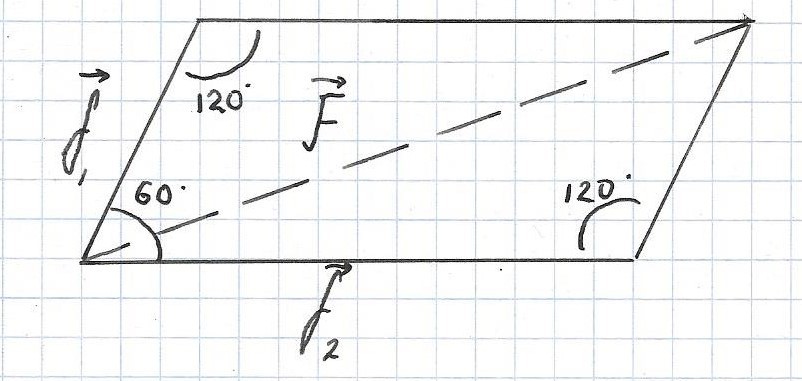

Due to the fact that opposite angles in a parallelogram equal each other, we know the angles inside are 60, 60, 120 and 120 degrees. Furthermore, as $\overrightarrow { { f }_{ 1 } }$ : $\overrightarrow { { f }_{ 2 } }$ , then they must also in ratio to $\overrightarrow { F }$ . We can use the cosine rule to find $\overrightarrow { F }$ . ${ a }^{ 2 }={ b }^{ 2 }+{ c }^{ 2 }-2bc\cos { A }$ $\therefore \quad \overrightarrow { { F }^{ 2 } } :\quad \overrightarrow { { f }_{ 1 }^{ 2 } } +\overrightarrow { { f }_{ 2 }^{ 2 } } -2{ f }_{ 1 }{ f }_{ 2 }\cos { 120 } \\ \overrightarrow { { F }^{ 2 } } :{ 2 }^{ 2 }+{ 3 }^{ 2 }-2(2)(3)\cos { 120 } \\ \overrightarrow { { F }^{ 2 } } =19\quad \therefore \quad \overrightarrow { F } =\sqrt { 19 }$

Therefore we may conclude that $\overrightarrow { { f }_{ 1 } } :\overrightarrow { { f }_{ 2 } } :\overrightarrow { F }$ so that $2:3:\sqrt { 19 }$ .

To find the remaining angles, all that remains is to use the Cosine Rule. $\cos { A } =\frac { { b }^{ 2 }+{ c }^{ 2 }-{ a }^{ 2 } }{ 2bc }$ . Substituting the correct values to find the angle enclosed by $\overrightarrow { { f }_{ 2 } }$ and $\overrightarrow { F }$ , we get $\cos ^{ -1 }{ \left( \frac { { (\sqrt { 19 } ) }^{ 2 }+{ 3 }^{ 2 }-{ 2 }^{ 2 } }{ 2\times \sqrt { 19 } \times 2 } \right) } =36.6°$ (3sf). This equals $y$ . Further more since $x+y$ must equal 60 degrees, $x=23.4°$ .

Therefore $y-x$ must equal 13.2.