Vector Sum
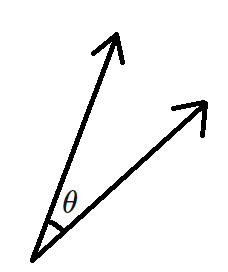
Two vectors of length in the 2D plane have an angular separation of . If the sum of the two vectors also has a length , by how many degrees are the two vectors separated?
Give your answer as a positive number between 0 and 180.
The answer is 120.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The solution can be obtained by using parallelogram law of vector addition .
We know if that if A , B are two Vectors then the resultant Vector would be
∣ ∣ ∣ ∣ R 2 ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ A 2 ∣ ∣ ∣ ∣ + ∣ ∣ ∣ ∣ B 2 ∣ ∣ ∣ ∣ + 2 A B c o s θ .
Now We can see that the case would be possible only if
2 cos θ = − 1
or cos θ = − 1 / 2 and cos 1 2 0 = − 1 / 2 . Hence the Angle θ = 1 2 0 .