Vectors and conic sections - Part 2
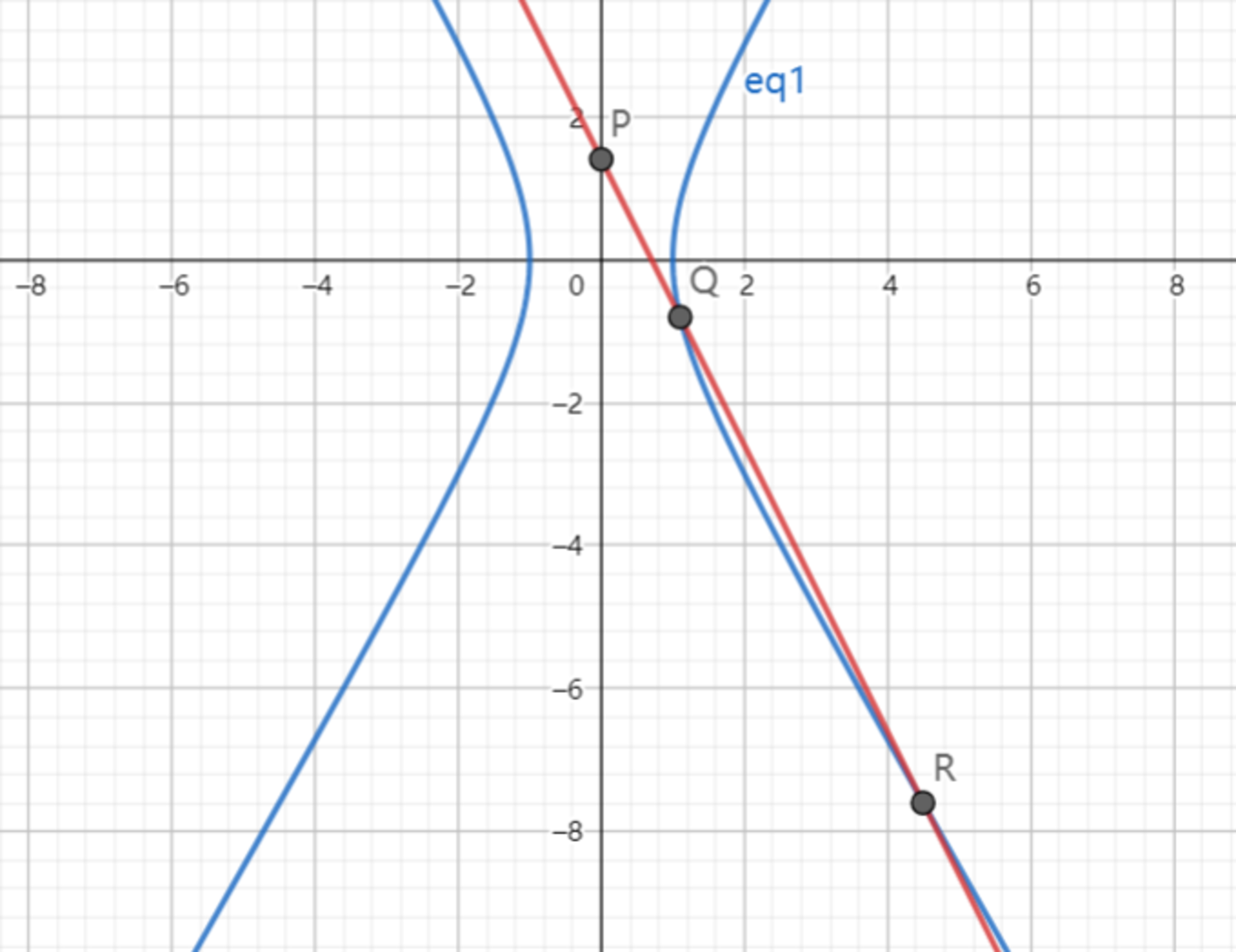
As shown above, the line: y = − 2 x + m intersects with the y -axis at point P and the right hand of the hyperbola: x 2 − 3 y 2 = 1 with point Q , R , and ∣ P Q ∣ < ∣ P R ∣ . Find the range of ∣ P Q ∣ ∣ P R ∣ .
If the range can be expressed as ( l , r ) , submit ⌊ 1 0 0 0 ( r − l ) ⌋ .
The answer is 12928.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Substituting y = − 2 x + m into x 2 − 3 y 2 = 1 gives x 2 − 3 ( − 2 x + m ) 2 = 1 , which solves to x = 2 m ± 3 m 2 − 3 .
This means the x -coordinate of Q is Q x = 2 m − 3 m 2 − 3 , and using y = − 2 x + m , the y -coordinate of Q is Q y = − 2 Q x + m , which simplifies to Q y = − 3 m + 2 3 m 2 − 3 .
Similarly, the x -coordinate of R is R x = 2 m + 3 m 2 − 3 , and using y = − 2 x + m , the y -coordinate of R is R y = − 2 R x + m , which simplifies to R y = − 3 m − 2 3 m 2 − 3 .
Since P is on the y -axis and on the line y = − 2 x + m , the coordinates of P are P x = 0 and P y = m .
The ratio k = ∣ P Q ∣ ∣ P R ∣ = ( Q x − P x ) 2 + ( Q y − P y ) 2 ( R x − P x ) 2 + ( R y − P y ) 2 , which simplifies to:
k = m 2 + 3 7 m 2 + 4 m 3 m 2 − 3 − 3
Since k is an increasing function for m > 0 , the lowest value of k occurs when the square root 3 m 2 − 3 = 0 , which is at m = 1 and k = 1 2 + 3 7 ⋅ 1 2 + 4 ⋅ 1 3 ⋅ 1 2 − 3 − 3 = 1 = l , and the highest value of k occurs at k = m → ∞ lim m 2 + 3 7 m 2 + 4 m 3 m 2 − 3 − 3 = m → ∞ lim m 2 m 2 + m 2 3 m 2 7 m 2 + m 4 m m 2 3 m 2 − m 2 3 − m 2 3 = 7 + 4 3 = r .
Therefore, r − l = ( 7 + 4 3 ) − 1 = 6 + 4 3 , so ⌊ 1 0 0 0 ( r − l ) ⌋ = ⌊ 1 0 0 0 ( 6 + 4 3 ) ⌋ = 1 2 9 2 8 .
Points Q ( x q , y q ) and R ( x r , y r ) satisfy both y = − 2 x + m and x 2 − 2 y 2 = 1 . Then we have:
3 x 2 − y 2 − 3 3 x 2 − ( 4 x 2 − 4 m x + m 2 ) − 3 x 2 − 4 m x + m 2 + 3 = 0 = 0 = 0
⟹ x = 2 4 m ± 1 6 m 2 − 4 m 2 − 1 2 = 2 m ± 3 ( m 2 − 1 )
⟹ x r = 2 m + 3 ( m 2 − 1 ) and x q = 2 m − 3 ( m 2 − 1 ) . Now we note that ∣ P Q ∣ ∣ P R ∣ = x q x r = 2 m − 3 ( m 2 − 1 ) 2 m + 3 ( m 2 − 1 ) . Its lowest bound is when m = 1 , then ∣ P Q ∣ ∣ P R ∣ = 1 . Its highest bound is when m → ∞ , then
∣ P Q ∣ ∣ P R ∣ = m → ∞ lim 2 m − 3 ( m 2 − 1 ) 2 m + 3 ( m 2 − 1 ) = m → ∞ lim 2 − 3 ( 1 − m 2 1 ) 2 + 3 ( 1 − m 2 1 ) = 2 − 3 2 + 3 = 7 + 4 3
Therefore, ⌊ 1 0 0 0 ( r − l ) ⌋ = ⌊ 1 0 0 0 ( 7 + 4 3 − 1 ) ⌋ = 1 2 9 2 8 .